 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1983 >> Районный тур >> 8 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1983. Районный тур. 8 класс |
|
|
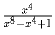 ,
если
,
если 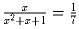 .
.Решение:
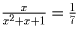 . Поделим на x числитель и
знаменатель левой части:
. Поделим на x числитель и
знаменатель левой части:  , откуда
, откуда 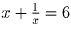 . После возведения в квадрат получаем
. После возведения в квадрат получаем
 , а затем
, а затем 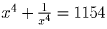 . Теперь найдём искомую дробь:
. Теперь найдём искомую дробь: 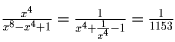 .
.Задача 2:
Задача 3: На одной стороне угла с вершиной O отложены равные отрезки OA = AB = BC, на другой стороне – равные отрезки OD = DE = EF. Докажите, что треугольники AEC и DBF равновелики.
Решение: У треугольников BEO и AEC равны основания AC = BO и общая высота из вершины E, значит, SBEO = SAEC. Аналогично SDBF = SOBE, значит, SAEC = SDBF.
Задача 4: Число членов арифметической прогрессии, разность которой отлична от нуля, четно, но не кратно 4. Сумма членов с четными номерами противоположна сумме членов с нечетными номерами. Докажите, что произведение всех членов прогрессии отрицательно.
Решение: Вычислим сумму членов прогрессии, стоящих на четных местах, и сумму членов, стоящих на нечетных местах:
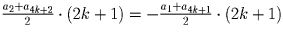 .
Отсюда получаем, что a2 + a4k + 2 = – (a1 + a4k + 1). При этом в
арифметической прогрессии
a1 + a4k + 2 = a2 + a4k + 1 = a3 + a4k + 2 = … . То есть все эти
суммы раны 0, а, значит отрицательных членов прогрессии ровно
половина, то есть 2k + 1. Следовательно произведение всех членов
прогрессии отрицаиельно.
.
Отсюда получаем, что a2 + a4k + 2 = – (a1 + a4k + 1). При этом в
арифметической прогрессии
a1 + a4k + 2 = a2 + a4k + 1 = a3 + a4k + 2 = … . То есть все эти
суммы раны 0, а, значит отрицательных членов прогрессии ровно
половина, то есть 2k + 1. Следовательно произведение всех членов
прогрессии отрицаиельно.Задача 5: Докажите, что для углов произвольного треугольника ABC справедливо равенство: sin ²A = sin ²B + sin ²C – 2 sin B sin C cos A.
Решение: Выразим синусы углов треугольника из теоремы синусов:
 , .
После такой замены доказываемое равенство превратится в теорему
косинусов.
, .
После такой замены доказываемое равенство превратится в теорему
косинусов.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1983 >> Районный тур >> 8 класс | Убрать решения |