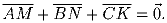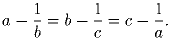Задача 1:
Существует ли целое число x такое, что x³ – 3x² + 2x + 1984 = 0?
Задача 2:
Точка D – середина основания BC равнобедренного треугольника
ABC. На отрезке AB взяли точку M так, что AM = ⅓AB. Найдите
∠ MCB, если известно, что AD = BC.
Задача 3:
Что больше:
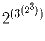
или
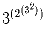
?
Задача 4:
На сторонах AB, BC и AC треугольника ABC вне него построены
квадраты; AM, BN, CK – стороны этих квадратов, перпендикулярные
сторонам AB, BC, AC соответственно.
Докажите, что
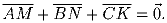
Задача 5:
Про вещественные числа a, b и c известно, что
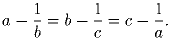
Докажите, что a = b = c.


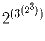 или
или 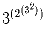 ?
?