Задача 1:
Докажите неравенство:
x² + y² + z² + 1 ≥ xy + yz + x + z
(x, y, z – вещественные числа).
Задача 2:
Задача 3:
Решить уравнение:
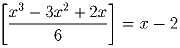
(квадратными скобками обозначена целая часть числа).
Задача 4:
Дана замкнутая ломанная A
1A
2A
3 … A
10; точки B
1,B
2, … ,B
10 –
середины ее звеньев, занумерованные в произвольном порядке.
Докажите, что
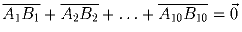
.
Задача 5:
ABCDA
1B
1C
1D
1 – куб с ребром 1м. На ребрах AA
1,AB,CD выбраны
соответственно точки K, L, M так, что AK = 95см., AL = 70см.,
CM = 26см. Пересекает ли плоскость KLM ребро C
1D
1?


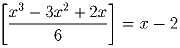
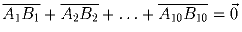 .
.