 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1985 >> Районный тур >> 10 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1985. Районный тур. 10 класс |
|
|
Задача 2: При каких целых a уравнение x4 – (a + 4)x² + (2a + 3) = 0 имеет целый корень?
Задача 3:
Задача 4: Докажите, что
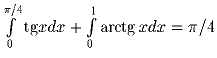 .
.Задача 5: Функция f(x) определена и имеет производную при всех вещественных значениях переменной, кроме того, при всех x выполнены равенства:
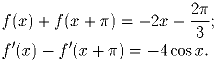
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1985 >> Районный тур >> 10 класс | Показать решения |