ЗАБА Математические олимпиады и олимпиадные задачи
Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1985 >> Районный тур >> 10 класс ФМШПоказать решения
Санкт-Петербургская (Ленинградская) математическая олимпиада. 1985. Районный тур. 10 класс ФМШ

Задача 1: Диагональные сечения правильной 8-угольной пирамиды, проведенные через наибольшую и наименьшую диагонали основания, равновелики. Под каким углом к основанию наклонена плоскость, проходящая через вершину пирамиды и наименьшую диагональ основания?

Задача 2: Найти уравнение прямой, касающейся графика функции y = x4 – 2x³ + x² + x – 2 в двух точках.

Задача 3:

Задача 4: Докажите, что .

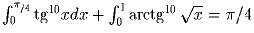Задача 5:

Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1985 >> Районный тур >> 10 класс ФМШПоказать решения