Задача 1:
Докажите, что дробь
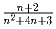
несократима ни при каком
натуральном n.
Задача 2:
Точки M и N выбраны на сторонах BC и CD квадрата ABCD так, что
лучи AM и AN делят угол BAD на три равные части. Высота ME
треугольника AMN продолжена до пересечения с отрезком CD в точке
F. Докажите, что треугольник DEF равнобедренный.
Задача 3:
Докажите, что при любых вещественных числах a и b хотя бы одно
из уравнений x² + 2ax + b = 0, ax² + 2bx + 1 = 0, bx² + 2x + a = 0 имеет
вещественный корень.
Задача 4:
Перемножив шесть последовательных натуральных чисел, получили
число *84933148400, первая цифра которого стерлась. Восстановите
эту цифру.


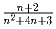 несократима ни при каком
натуральном n.
несократима ни при каком
натуральном n.