Задача 1:
Докажите, что дробь
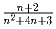
несократима ни при каком
натуральном n.
Решение: Записав заменатель в виде n² + 4n + 3 = (n + 2)² – 1, заметим, что общим
делителем числителя и знаменателя может быть только ± 1, то есть
дробь несократима.
Задача 2:
Точки M и N выбраны на сторонах BC и CD квадрата ABCD так, что
лучи AM и AN делят угол BAD на три равные части. Высота ME
треугольника AMN продолжена до пересечения с отрезком CD в точке
F. Докажите, что треугольник DEF равнобедренный.
Решение:
Продолжим MF до пересечения с продолжением стороны AD в точке
X. ∠ MAD = ⅔ ∠ BAD = 60, ∠ AME = 60
(из прямоугольного треугольника AME). Тогда треугольник AMX
равносторонний, и AX = AM. Поскольку AM = AN, треугольник NAX
равнобедренный. ND и XE – высоты к боковым сторонам
равнобедренного треугольника. Значит, F – их точка
пересечения – лежит на оси симметрии треугольника ANX.
Следовательно, FE = FD. Что и требовалось.
Задача 3:
Докажите, что при любых вещественных числах a и b хотя бы одно
из уравнений x² + 2ax + b = 0, ax² + 2bx + 1 = 0, bx² + 2x + a = 0 имеет
вещественный корень.
Решение:
Пусть первые два уравнения не имеют вещественных корней, тогда
их дискриминанты отрицательны: a² – b < 0 и b² – a < 0. Перепишем неравенства
в виде a² < b,b² < a и, заметив, что a и b
положительны, перемножим их: a²b² < ab; ab < 1.
Это означает, что дискриминант третьего уравнения
положителен. Значит, хотя бы одно из уравнений имеет вещественный
корень.
Задача 4:
Перемножив шесть последовательных натуральных чисел, получили
число *84933148400, первая цифра которого стерлась. Восстановите
эту цифру.
Решение:
Среди шести последовательных натуральных чисел есть одно,
делящееся на 6, и кроме него ещё одно, делящее на 3.
Тогда их произведение будет делиться на 9.
Воспользовавшись признаком делимости на 9, получаем,
что стерта цифра 1.


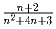 несократима ни при каком
натуральном n.
несократима ни при каком
натуральном n.