 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1985 >> Районный тур >> 8 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1985. Районный тур. 8 класс |
|
|
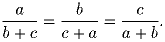
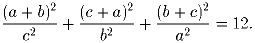
Задача 2: Из каждой вершины 4-угольника провели векторы к серединам всех его сторон. Докажите, что сумма шестнадцати образовавшихся векторов равна
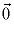 .
.Задача 3: Докажите, что дробь
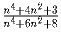 несократима ни при каких
целых n.
несократима ни при каких
целых n.Задача 4: На стороне AB треугольника ABC взяли точку M такую, что AM = ⅓AB. В каком отношении отрезок CM делит медиану, проведенную из вершины A?
Задача 5:
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1985 >> Районный тур >> 8 класс | Показать решения |