 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1986 >> Районный тур >> 10 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1986. Районный тур. 10 класс |
|
|
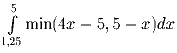 .
.Задача 2:
Задача 3:
Задача 4: M – произвольная точка основания ABC тетраэдра ABCD. Через точку M проведены сечения параллельные боковым граням. Пусть S1, S2 и S3 – площади боковых граней; x, y, z – площади соответствующих сечений. Докажите, что
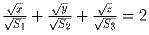 .
.Задача 5:
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1986 >> Районный тур >> 10 класс | Показать решения |