Задача 1: Площадь прямоугольного треугольника равна 7, 5 см², а его периметр равен 15 см. Найдите стороны треугольника.

Задача 2: Докажите, что если 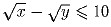, то x – 2y ≤ 200.

Задача 3: Могут ли шесть попарных сумм четырех вещественных чисел совпадать с числами 3, 4, 4, 5, 6, 8?

Задача 4: Вычислить .

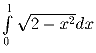Задача 5: В треугольной пирамиде ABCD ребра AB,BC,CD попарно перпендикулярны. Докажите, что шесть середин ребер пирамиды не могут лежать на одной сфере.