Задача 1:
Существуют ли целые числа a,b,c, для которых
(3a – b)(3b – c)(3c – a) = 5005?
Решение:
Сумма чисел 3a – b; 3b – c; 3c – a чётна, значит хотя бы
одно из них четно. Тогда их произведение тоже чётно и не может
равняться 5005.
Задача 2:
Две окружности касаются внешним образом в точке A. К
окружностям проведены параллельные касательные: к первой в
точке B, ко второй в точке C, причем точка A не лежит между
касательными. Докажите, что угол BAC прямой.
Решение:
Пусть O
1 и O
2 центры окружностей; проведем общую
касательную в точке A. Она разобьет угол BAC на части, равные
половинам дуг, отсекаемых хордами AB и AC.
Значит, ∠ BAC = ½( ∠ BO
1A + ∠ CO
2A) = 90
(поскольку углы BO
1A и CO
2A – внутренние
односторонние при параллельных прямых BO
1 и CO
1).
Задача 3:
Могут ли шесть попарных разностей для четырех чисел совпадать
с числами 2, 2, 3, 4, 5, 6?
Решение:
Если все числа одной чётности, то нечётных разностей быть не
может. Если ровно три числа одной чётности, то нечётных разностей
должно быть три. Если чётных и нечётных чисел по два, то должно быть
четыре нечётных разности. Значит чисел с попарными
разностями 2, 2, 3, 4, 5, 6 не существует.
Задача 4:
Задача 5:
Пусть M и K – точки на сторонах AC и BC треугольника
ABC, O – точка пересечения отрезков AK и BM. Найдите
площадь треугольника ABC, если треугольники AMO и BKO имеют
площадь 8, а треугольник KMO имеет площадь 4.
Решение:
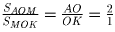
,
значит S
BOA = S
BOK • 2 = 16;
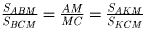
, то есть

, откуда S
MKC = 12.
Теперь находим, что S
ABC = 48.


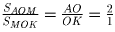 ,
значит SBOA = SBOK • 2 = 16;
,
значит SBOA = SBOK • 2 = 16; 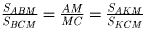 , то есть
, то есть
 , откуда SMKC = 12.
Теперь находим, что SABC = 48.
, откуда SMKC = 12.
Теперь находим, что SABC = 48.