Задача 1:
Задача 2:
Задача 3:
Задача 4:
С натуральным числом разрешается проводить следующие две
операции: удвоение и стирание последней цифры. Докажите, что с
помощью таких операций можно из любого натурального числа
получить любое другое натуральное число.
Решение:
Из любого числа можно получить однозначное, из которого легко
получить единицу. Теперь достаточно показать, что для любого N
существует степень двойки, начало которой совпадает с числом N, то
есть существуют такие m и k, что N • 10
m ≤ 2
k < (N + 1) • 10
m. Прологарифмируем:
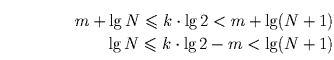
Пусть α < α
1 – дробные части
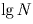
и

соответственно.
Так как
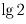
иррационален, то найдется сколь угодно большое k
такое, что дробная часть
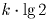
попадет в интервал ( α , α
1). Возьмем k таким большим, чтобы
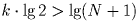
и подберем m так, чтобы было выполнено наше
неравенство. В случае α > α
1 поступим также, только
вместо ( α , α
1) будем рассматривать интервал ( α , α
1 + 1). Осталось заметить, что α и α
1
всегда различны, таким образом все случаи рассмотрены.
Задача 5:
Тетраэдр ABCD и точка M в пространстве таковы, что результатом
последовательного отражения точки M относительно всех граней
тетраэдра и вершины A будет вновь точка M. Докажите, что в
тетраэдре имеется вершина такая, что все двугранные углы между
сходящимися в ней гранями прямые.
Решение:
Аналогично задаче 24.


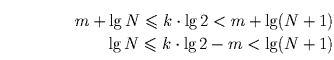
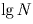 и
и  соответственно.
Так как
соответственно.
Так как 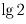 иррационален, то найдется сколь угодно большое k
такое, что дробная часть
иррационален, то найдется сколь угодно большое k
такое, что дробная часть 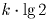 попадет в интервал ( α , α 1). Возьмем k таким большим, чтобы
попадет в интервал ( α , α 1). Возьмем k таким большим, чтобы 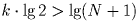 и подберем m так, чтобы было выполнено наше
неравенство. В случае α > α 1 поступим также, только
вместо ( α , α 1) будем рассматривать интервал ( α , α 1 + 1). Осталось заметить, что α и α 1
всегда различны, таким образом все случаи рассмотрены.
и подберем m так, чтобы было выполнено наше
неравенство. В случае α > α 1 поступим также, только
вместо ( α , α 1) будем рассматривать интервал ( α , α 1 + 1). Осталось заметить, что α и α 1
всегда различны, таким образом все случаи рассмотрены.