Задача 1: Числа a₁,a₂, … ,a_n образуют арифметическую прогрессию, также как и числа  sin a₁,  sin a₂,  … ,  sin a_n, причем  sin a₁ = ½, sin a_n =  – ½. Чему равно число  sin a₂?

Задача 2: На необитаемом острове пираты закопали клад, причем они запомнили, что если от Южного Мыса пройти 70 метров налево по прямой вдоль берега, а затем пройти 110 метров по направлению ко вкопанному столбу, то окажешься на месте, где зарыт клад. Точно так же можно попасть на это место, если от Южного Мыса пройти 130 метров к столбу, а затем повернуть направо и пройти 10 метров. Когда пираты вновь приехали на остров, то обнаружили, что столб вырвало бурей. Как им теперь найти клад?

Задача 3: Решить в вещественных числах систему уравнений:

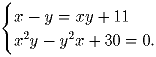
Задача 4: Найдите все такие натуральные x, что x³ + 7 делится на x – 2.

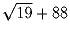
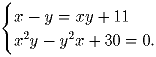
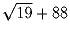Задача 5: Микрокалькулятор «Чебурашка» умеет складывать, вычитать и находить по данному числу x обратное к нему число 1/x. Можно ли с помощью этого микрокалькулятора получить число 1, имея число (имеется в виду, что вводить в микрокалькулятор числа, отличные от данных или полученных в результате вычислений, запрещается).