Задача 1:
Найдите все натуральные числа x такие, что x³ + 3 делится на
x² – x + 1.
Задача 2:
Треугольник ABC и точка M на плоскости таковы, что результатом
последовательного отражения точки M относительно всех сторон
треугольника и вершины A будет снова точка M. Докажите, что
треугольник ABC – прямоугольный.
Задача 3:
Действительные числа A, B, C таковы, что
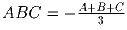
. Доказать, что абсолютная величина хотя бы
одного из чисел A, B, C не превосходит
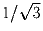
.
Задача 4:
Ломаная линия на поверхности тетраэдра содержит все его
вершины и середины ребер. Какое наименьшее число звеньев может
содержать эта ломаная?
Задача 5:
Можно ли с помощью микрокалькулятора "Чебурашка", который
умеет складывать, вычитать и находить по данному числу x
обратное к нему число 1/x получить единицу имея исходно число:



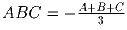 . Доказать, что абсолютная величина хотя бы
одного из чисел A, B, C не превосходит
. Доказать, что абсолютная величина хотя бы
одного из чисел A, B, C не превосходит 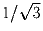 .
.