 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1988 >> Районный тур >> 9 класс ФМШ | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1988. Районный тур. 9 класс ФМШ |
|
|
Решение:
 ;
;  ,
значит,
,
значит, 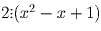 и x² – x + 1 может принимать
лишь значения ± 1; ± 2, откуда x = 0 или x = 1.
Задача 2:
Треугольник ABC и точка M на плоскости таковы, что результатом
последовательного отражения точки M относительно всех сторон
треугольника и вершины A будет снова точка M. Докажите, что
треугольник ABC – прямоугольный.
и x² – x + 1 может принимать
лишь значения ± 1; ± 2, откуда x = 0 или x = 1.
Задача 2:
Треугольник ABC и точка M на плоскости таковы, что результатом
последовательного отражения точки M относительно всех сторон
треугольника и вершины A будет снова точка M. Докажите, что
треугольник ABC – прямоугольный.Решение: Пусть M1, M2, M3 – образы точки M при последовательных отражениях. Три из четырёх проделанных преобразований (симметрии относительно прямой AB, прямой AC и точки A) не меняют расстояния до точки A. Поскольку точка M осталась на месте, то и симметрия относительно BC не изменила расстояния до точки A. Значит одна из точек Mi лежит на прямой BC. Последовательные отражения относительно AC и AB есть поворот на 2 ∠ BAC, а отражение относительно точки A – поворот на 180 . Значит, композиция всех этих преобразований является поворотом точки M на 2 ∠ BAC + 180 . Так как M осталось неподвижна, то 2 α + 180 делится на 2 π . Значит, ∠ BAC = 90 . Задача 3: Действительные числа A, B, C таковы, что
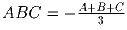 . Доказать, что абсолютная величина хотя бы
одного из чисел A, B, C не превосходит
. Доказать, что абсолютная величина хотя бы
одного из чисел A, B, C не превосходит 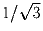 .
.Решение: Заметим, что из чисел A, B, C, ровно два числа одного знака. Пусть A,B > 0, C < 0. Обозначим – C = D > 0 и перепишем условие в виде
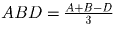 . Предположим, что
. Предположим, что
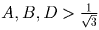 и заметим, что тогда
и заметим, что тогда 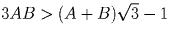 (следует из того, что
(следует из того, что 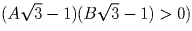 .
Тогда
.
Тогда
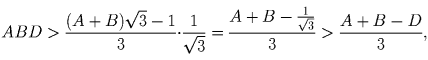
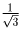 .
Задача 4:
Ломаная линия на поверхности тетраэдра содержит все его
вершины и середины ребер. Какое наименьшее число звеньев может
содержать эта ломаная?
.
Задача 4:
Ломаная линия на поверхности тетраэдра содержит все его
вершины и середины ребер. Какое наименьшее число звеньев может
содержать эта ломаная?Решение: Пример ломанной, содержащей 6 звеньев изображен на рисунке. Предположим, нашлась аналогичная ломанная из пяти звеньев. Тогда рассмотрим её ребро, содержащее две из шести середин ребер (следовательно, на нем нет больше отмеченных точек). Ребро, соседнее с этим, содержит ещё только одну отмеченную точку, а остальные ещё не более чем по две точки. Всего точек не более, чем 2 + 1 + 2 + 2 + 2 = 9 < 10. Значит, пяти звенной ломанной быть не может. Задача 5: Можно ли с помощью микрокалькулятора "Чебурашка", который умеет складывать, вычитать и находить по данному числу x обратное к нему число 1/x получить единицу имея исходно число:

Решение: a) Из числа x можно получить все нечетные степени x, пользуясь тождеством.
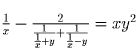 при x = y. Таким образом
из
при x = y. Таким образом
из 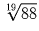 можно получить 88, затем
можно получить 88, затем  , из
которой легко получается единица.
, из
которой легко получается единица.b) Нельзя, так как калькулятор из числа
 (a,b – рациональны) получает число
такого же вида.
(a,b – рациональны) получает число
такого же вида.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1988 >> Районный тур >> 9 класс ФМШ | Убрать решения |