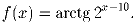Задача 1: Трапеция ABCD такова, что круги, построенные на ее боковых сторонах как на диаметрах, касаются друг друга. Докажите, что в ABCD можно вписать окружность.

Задача 2: Дана функция

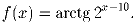
Найдите сумму f(0) + f(1) +  …  + f(20).

Задача 3: Действительные числа x, y, z таковы, что x² + y² + z² = 3(x + y + z). Каково минимальное значение, которое может при этом принимать выражение xy + yz + xz?

Задача 4: Длины сторон треугольника, лежащего в основании пирамиды, равны 10, 10 и 12, а боковые грани образуют с основанием двугранные углы, равные 30  . Найдите высоту пирамиды.

Задача 5: