Задача 1:
ABCD – произвольный четырехугольник. Пусть K,L,M,N –
середины сторон AB,BC,CD,DA соответственно. Докажите, что
сумма векторов
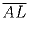
,
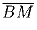
,
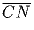
,
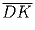
равна нуль-вектору.
Задача 2:
Вещественные числа a, b и c таковы, что abc = a + b + c. Докажите,
что
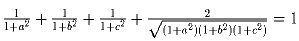
.
Задача 3:
Задача 4:
Данные точки A и B лежат по одну сторону от данной прямой L.
Постройте на прямой L точку X такую, что прямая XA является
биссектрисой угла, образованного прямыми L и XB.
Задача 5:
Найдите все пары простых чисел p и q, удовлетворяющих
уравнению p² + q = 37q² + p.


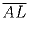 ,
, 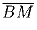 ,
, 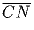 ,
, 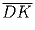 равна нуль-вектору.
равна нуль-вектору.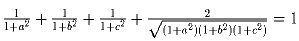 .
.