 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1994 >> Городской тур >> 10 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1994 года. Городской тур. 10 класс |
|
|
(С.Л.Берлов и др.)
Задача 2: Назовем треугольник «невысоким», если по крайней мере две его высоты имеют длину, не большую 1. На плоскости даны четыре точки такие, что все образуемые ими треугольники – невысокие. Докажите, что существует прямая, от которой все эти точки удалены на расстояние, не превосходящее 1/2.(С.Л.Берлов)
Задача 3: Натуральные числа a1, b1, c1, a2, b2 и c2 таковы, что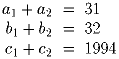
(А.Е.Перлин)
Задача 4: На полке стоят 1994 тома энциклопедии. Каждое утро библиотекарь Федя берет три тома и как-то расставляет их на тех же местах, а каждый вечер уборщица Дуся меняет какие-то два тома местами. Докажите, что Дуся может действовать так, что в любой момент времени на своих местах будет стоять менее пяти томов (исходно тома расставляет уборщица).
(Ф.Л.Назаров)
Задача 5: На сторонах AB, BC и CA произвольного треугольника ABC взяты точки C1, A1 и B1 соответственно. Обозначим через S1, S2 и S3 площади треугольников AB1C1, BA1C1 и CA1B1 соответственно. Докажите, что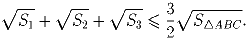
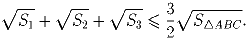
(С.Л.Берлов)
Задача 6: Квадрат разбит на несколько прямоугольников так, что любая горизонтальная прямая пересекает ровно n прямоугольников, а любая вертикальная прямая – ровно m прямоугольников (рассматриваются только прямые, не содержащие сторон прямоугольников). Каково минимально возможное число прямоугольников разбиения?
(Д.В.Карпов)
Задача 7: Двое играют в игру. Первый игрок загадал число, а второй игрок за ход может назвать любые пять различных натуральных чисел, не больших 9, после чего первый сообщает сумму задуманного числа и одной из названных цифр. За какое минимальное число ходов второй может отгадать задуманное число?(С.Л.Берлов)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1994 >> Городской тур >> 10 класс | Показать решения |