 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1994 >> Городской тур >> 11 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1994 года. Городской тур. 11 класс |
|
|
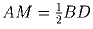 .
.
(С.Л.Берлов)
Задача 2: На острове, население которого составляют только рыцари, всегда говорящие правду, и лжецы, которые всегда лгут, находится НИИ. Каждый из его сотрудников однажды сделал два заявления:а) В институте нет и десяти человек, которые работают больше меня.
б) По крайней мере сто человек в институте получают зарплату большую, чем моя.
Известно, что нагрузка у всех работников разная, как и зарплата. Сколько человек работает в НИИ?
(Ф.Л.Назаров)
Задача 3: Натуральные числа a, b, x и y таковы, что ax + by делится на a² + b². Докажите, что числа x² + y² и a² + b² имеют общий делитель, больший 1.(А.Е.Перлин)
Задача 4: На полке стоят 1994 тома энциклопедии. Каждое утро библиотекарь Федя берет три тома и как-то расставляет их на тех же местах, а каждый вечер уборщица Дуся меняет какие-то два тома местами. Докажите, что Дуся может действовать так, что в любой момент времени на своих местах будет стоять менее пяти томов (исходно тома расставляет уборщица).
(Ф.Л.Назаров)
Задача 5: Точка H – ортоцентр треугольника ABC, а точки H1 и H2 – ее проекции на биссектрисы внутреннего и внешнего углов B. Докажите, что прямая H1H2 делит сторону AC пополам.
(Д.В.Фомин)
Задача 6: Квадрат разбит на несколько прямоугольников так, что любая горизонтальная прямая пересекает ровно n прямоугольников, а любая вертикальная прямая – ровно m прямоугольников (рассматриваются только прямые, не содержащие сторон прямоугольников). Каково минимально возможное число прямоугольников разбиения?(Д.В.Карпов)
Задача 7: Дана конечная последовательность чисел a1, a2, …, an. Разрешается для любого k < n заменить внутри последовательности числа a1, a2, …, ak на числа ak + 1 – ak, ak + 1 – ak – 1, …, ak + 1 – a1 (в указанном порядке). Докажите, что при помощи таких операций можно получить единственную последовательность чисел, в которой каждое число, кроме последнего, не меньше полусуммы своих соседей.
(С.Л.Берлов)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1994 >> Городской тур >> 11 класс | Показать решения |