 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1994 >> Городской тур >> 6 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1994 года. Городской тур. 6 класс |
|
|
(Д.В.Фомин)
Задача 2: На шахматной доске расставлены ладьи так, что на каждой вертикали и на каждой горизонтали находится ровно одна ладья. Доску разбили на четыре равных квадрата. Докажите, что число ладей в правом верхнем квадрате равно числу ладей в левом нижнем квадрате.(С.Л.Берлов)
Задача 3: На каждой из одиннадцати карточек написано по цифре, не превосходящей пяти. Расположив эти карточки в ряд, Миша получил одно 11-значное число; затем, расположив те же карточки по-другому, Миша получил второе 11-значное число. Докажите, что сумма двух этих чисел будет содержать хотя бы одну четную цифру в своей десятичной записи.(Р.А.Семизаров)
Задача 4: При дворе принца Лимона служили герцоги, графы и бароны. В начале правления принца придворных было 1994, но каждый день один из них убивал другого на дуэли, причем герцоги убивали только графов, графы – только баронов, а бароны – только герцогов. При этом никто не выиграл дуэль дважды. В конце концов остался в живых лишь барон Апельсин. Какой титул был у первого погибшего придворного?(А.Е.Перлин)
Задача 5: У Кости есть 222 ромба вида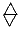 , 333 треугольника
, 333 треугольника
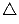 и 444 трапеции вида
и 444 трапеции вида  , причем все отрезки на
рисунках имеют длину 1. Докажите, что Костя не сможет сложить
многоугольник периметра 888, использовав при этом все плитки. При
складывании стороны фигурок должны точно совмещаться.
, причем все отрезки на
рисунках имеют длину 1. Докажите, что Костя не сможет сложить
многоугольник периметра 888, использовав при этом все плитки. При
складывании стороны фигурок должны точно совмещаться.
(К.П.Кохась)
Задача 6: На доске выписано в ряд 101 натуральное число. За один ход разрешается из любых двух соседних чисел вычесть по единице. Известно, что такими операциями можно получить наборы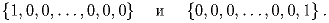
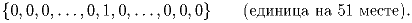
(А.Е.Перлин)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1994 >> Городской тур >> 6 класс | Показать решения |