 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1994 >> Городской тур >> 8 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1994 года. Городской тур. 8 класс |
|
|
(С.В.Иванов)
Задача 2: При дворе принца Лимона служили герцоги, графы и бароны. В начале правления принца придворных было 1994, но каждый день один из них убивал другого на дуэли, причем герцоги убивали только графов, графы – только баронов, а бароны – только герцогов. При этом никто не выиграл дуэль дважды. В конце концов остался в живых лишь барон Апельсин. Какой титул был у первого погибшего придворного? Задача 3: Дано 15-значное число, записанное нулями и единицами, которое делится на 81, но не делится на 10. Докажите, что из него нельзя вычеркнуть один из нулей так, чтобы полученное число по-прежнему делилось на 81.(М.Н.Гусаров, С.Л.Берлов)
Задача 4: Есть сто монет достоинством 1, 2, 3,…, 100 пиастров. Среди них ровно 16 фальшивых, то есть таких, что их вес в граммах не равен их достоинству. Как при помощи чашечных весов без гирь найти все фальшивые монеты?(Д.В.Фомин, М.Н.Гусаров)
Задача 5: Найдите все натуральные числа n, для которых сумма квадратов всех их собственных (т.е., не равных n) делителей равна 2n + 2.(Д.В.Фомин)
Задача 6: Тушенка продается в банках пяти типов – они различаются по весу и цене (см. таблицу). На складе имеется 1994 банки общим весом 1 тонна. Докажите, что их общая стоимость меньше 1.600.000 рублей.
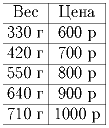
(К.П.Кохась)
Задача 7: Бумажный квадрат разбит линиями, проведенными карандашом, на n прямоугольников. Докажите, что можно сделать не более n – 1 прямолинейного разреза, после которых бумажный квадрат распадется в точности на нарисованные прямоугольники. Части нельзя накладывать друг на друга, а разрез не обязан начинаться или кончаться на краю.(С.В.Иванов)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1994 >> Городской тур >> 8 класс | Показать решения |