 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1994 >> Городской тур >> 9 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1994 года. Городской тур. 9 класс |
|
|
а) В институте нет и десяти человек, которые работают больше меня.
б) По крайней мере сто человек в институте получают зарплату большую, чем моя.
Известно, что нагрузка у всех работников разная, как и зарплата. Сколько человек работает в НИИ?
(Ф.Л.Назаров)
Задача 2: Натуральные числа p и q таковы, что p ≥ q. У ослика Иа-Иа есть pq палочек, из которых он может составить p q-угольников. Докажите, что из этих же палочек Иа-Иа может составить q p-угольников.(Ф.Л.Назаров)
Задача 3: AL – биссектриса треугольника ABC, K – точка на стороне AC такая, что CK = CL. Прямая LK и биссектриса угла B пересекаются в точке P. Докажите, что AP = PL.
(С.Л.Берлов)
Задача 4: Про натуральные числа a, b, c и d известно, что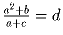 . Докажите, что d ≤ b + (c – 1)².
. Докажите, что d ≤ b + (c – 1)².
(С.Л.Берлов)
Задача 5: Двое играют в игру. Первый игрок загадал число, а второй игрок за ход может назвать любые k различных натуральных чисел, не больших 100, после чего первый сообщает сумму задуманного числа и одного из названных чисел. При каком максимальном k второй сможет рано или поздно отгадать задуманное число?
(С.Л.Берлов, Ф.Л.Назаров)
Задача 6: Квадрат разбит на несколько прямоугольников так, что любая горизонтальная прямая пересекает ровно n прямоугольников, а любая вертикальная прямая – ровно m прямоугольников (рассматриваются только прямые, не содержащие сторон прямоугольников). Каково минимально возможное число прямоугольников разбиения?(Д.В.Карпов)
Задача 7: На сторонах AB, BC, CD и DA произвольного четырехугольника ABCD взяты точки K, L, M и N соответственно. Обозначим через S1, S2, S3 и S4 площади треугольников AKN, BKL, CLM и DMN соответственно. Докажите, что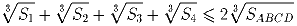
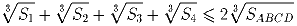
(С.Л.Берлов)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1994 >> Городской тур >> 9 класс | Показать решения |