Задача 1: В точках A и B, лежащих на разных сторонах угла, восстановлены перпендикуляры к сторонам, которые пересекают биссектрису угла в точках C и D. Докажите, что середина отрезка CD равноудалена от точек A и B.

(С.В.Иванов)

Задача 2: Натуральные числа a, b и n > 1 таковы, что (a + b)ⁿ делится на ab. Докажите, что a^n – 1 делится на b.

(С.Л.Берлов)

Задача 3: Отрезки, соединяющие точку P, лежащую внутри квадрата ABCD, с вершинами, разбивают квадрат на четыре треугольника. Докажите, что отношение площадей каких-то двух из них лежит в промежутке .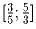

(С.Л.Берлов)

Задача 4: На доске написано число 1994. Каждую секунду к числу на доске прибавляют его максимальный простой делитель. Докажите, что когда-нибудь это число будет делиться на 1995.

(А.С.Голованов)

Задача 5: В неравнобедренном остроугольном треугольнике ABC взята точка O такая, что  ∠ OBC =  ∠ OCB = 20. Кроме того,  ∠ BAO +  ∠ OCA = 70. Найдите угол A.

(С.Л.Берлов)

Задача 6: В клетках таблицы 1995 × 1995 расставлены плюсы и минусы. Разрешается выбрать 1995 клеток, никакие две из которых не лежат в одной строке или в одном столбце, и поменять знаки в выбранных клетках. Докажите, что при помощи таких операций можно добиться того, чтобы в таблице осталось не более 1994 плюсов.

(Д.В.Карпов)

Задача 7: Рассматриваются последовательности натуральных чисел (a_n) длины 1994, обладающие следующим свойством: a₁ = 1, a_n + 1 ≤ 1 + a_n. Докажите, что количество таких последовательностей с четной суммой членов равно количеству последовательностей с нечетной суммой членов.

(Д.В.Карпов)

Задача 8: 200 теннисистов проводят турнир по швамбранской системе. Это означает, что каждый день перед очередными играми они выстраиваются в шеренгу по невозрастанию количества набранных к этому моменту очков, после чего разбиваются на 100 пар стоящих рядом игроков. Докажите, что если турнир длится достаточно долго, то в какой-то день результаты некоторых двух игроков будут различаться более, чем на 50 очков. (Ничьих в теннисе не бывает, за победу теннисист получает 1 очко, за поражение – 0).

(С.Л.Берлов)