 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Городской тур >> 10 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1995 года. Городской тур. 10 класс |
|
|
(С.~Берлов)
Задача 2: Внутри параллелограмма ABCD выбрана точка O так, что ∠ OAD = ∠ OCD. Докажите, что ∠ OBC = ∠ ODC.(С.~Берлов)
Задача 3: Шахматная фигура «пулеметчик» бьет в каком-то одном направлении по вертикали или горизонтали (например, по горизонтали влево) на любое число клеток. Какое наибольшее количество не бьющих друг друга пулеметчиков можно расставить на шахматной доске 20 × 20?(А.~Пастор)
Задача 4: Пусть d(n) – количество натуральных делителей числа n. Можно ли выбрать сто натуральных чисел a1,a2, … ,a100 так, чтобы при всех k от 1 до 100 выполнялось равенство d(a1 + a2 + … + ak) = ak?(Н.~Филонов)
Задача 5: В треугольнике ABC на сторонах AB и BC выбраны точки K и L соответственно, так, что ∠ KCB = ∠ LAB = α . Из точки B опущены перпендикуляры BD и BE на прямые AL и CK соответственно. Точка F – середина стороны AC. Найдите углы треугольника DEF.(С.~Берлов)
Задача 6: В государстве 2000 городов. Некоторые пары городов соединены дорогами так, что из любого города можно проехать в любой другой. Докажите, что это государство можно разбить на несколько республик (возможно, всего на одну) так, чтобы в каждой республике из любого города можно было единственным образом проехать в любой другой город этой республики, не выезжая за ее пределы. (В каждой республике должно быть не менее двух городов.)
(Д.~Карпов, А.~Пастор)
Задача 7: В последовательности натуральных чисел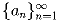 сумма
первых десяти членов равна 100, а начиная с a11, каждое число an равно количеству i < n, таких, что ai + i ≥ n. Известно, что
a11 = 10. Докажите, что начиная с некоторого места все члены последовательности равны между собой.
сумма
первых десяти членов равна 100, а начиная с a11, каждое число an равно количеству i < n, таких, что ai + i ≥ n. Известно, что
a11 = 10. Докажите, что начиная с некоторого места все члены последовательности равны между собой.
(С.~Берлов)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Городской тур >> 10 класс | Показать решения |