 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Городской тур >> 11 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1995 года. Городской тур. 11 класс |
|
|
(А.~Голованов; рис.~Т.~Кохась)
Решение: Проверьте, например, что 1728-й новобранец не попадет ни в один из нарядов (1728 = 12³).Задача 2: a1,a2, … ,an – натуральные числа, N – их произведение. Известно, что N делится на квадрат каждого из чисел a1, … ,an. Для каждой пары (i,j), i < j вычислили наибольший общий делитель чисел ai и aj; M – произведение всех этих наибольших общих делителей. Докажите, что M² делится на N.
(С.~Берлов, С.~Иванов)
Решение: Наибольший общий делитель чисел ai и aj будем, как обычно, обозначать (ai,aj). Условие задачи означает, что каждое ai делит произведение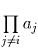 . Это произведение будет делиться на ai,
даже если каждый множитель aj
заменить на (aj,ai). Действительно, отбрасываемые при этом части
разложения aj на простые сомножители не влияют на делимость на ai
(в число
. Это произведение будет делиться на ai,
даже если каждый множитель aj
заменить на (aj,ai). Действительно, отбрасываемые при этом части
разложения aj на простые сомножители не влияют на делимость на ai
(в число 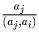 входят простые множители либо не входящие
в ai, либо такие, количество которых в разложении (aj,ai) уже
равно количеству в разложении ai). Таким образом, для каждого
фиксированного i
входят простые множители либо не входящие
в ai, либо такие, количество которых в разложении (aj,ai) уже
равно количеству в разложении ai). Таким образом, для каждого
фиксированного i 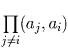 делится на ai.
Перемножая по всем i, получаем, что
делится на ai.
Перемножая по всем i, получаем, что  делится на
делится на 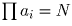 .
.Задача 3: Внутри параллелограмма ABCD выбрана точка O так, что ∠ OAD = ∠ OCD. Докажите, что ∠ OBC = ∠ ODC.
(С.~Берлов)
Решение: Эта задача имеет много решений. Мы приведем лишь некоторые.Решение 1. Построим отрезок OE, равный по длине и параллельный отрезку AD. Тогда AOED – параллелограмм, следовательно, ∠ OED = ∠ OAD = ∠ OCD, и четырехугольник OCED – вписанный. Значит, ∠ ODC = ∠ OEC, как опирающиеся на одну и ту же хорду. Но четырехугольник OBCE – тоже параллелограмм. Поэтому ∠ OEC = ∠ OBC, откуда и следует утверждение задачи.
Решение 2. Заметим, что ∠ BAO = ∠ BCO. Обозначим ∠ OAD = ∠ OED = α , ∠ ODC = β , ∠ OBC = δ , ∠ ADC = ∠ ABC = γ . Тогда ∠ ADO = γ – β , ∠ ABO = γ – δ . Напишем теоремы синусов для треугольников AOD и OED:

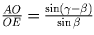 . Аналогично из
теорем синусов для треугольников AOB и BOC получаем, что
. Аналогично из
теорем синусов для треугольников AOB и BOC получаем, что
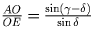 . Значит,
. Значит,
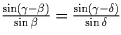 .
Это равенство легко приводится к виду
.
Это равенство легко приводится к виду sin ( β – δ ) = 0. Значит, β = δ .
Решение 3. Проведем через точку O прямые, параллельные сторонам
параллелограмма. Пусть K, L, M, N – точки пересечения этих прямых со
сторонами параллелограмма (см. рисунок). Прямые разбивают исходный
параллелограмм на четыре параллелограмма, так что на полученной картинке
образовалось много равных отрезков и углов.
Заметим, что треугольники AON и COM подобны,
поэтому 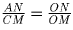 .
В треугольниках BLO и OMD ∠ L = ∠ M, и при этом
.
В треугольниках BLO и OMD ∠ L = ∠ M, и при этом
 . Значит, эти
треугольники подобны, и ∠ LBO = ∠ ODM, что и требовалось доказать.
. Значит, эти
треугольники подобны, и ∠ LBO = ∠ ODM, что и требовалось доказать.
(А.~Пастор)
Решение: Ответ: 76 пулеметчиков. Пример расстановки: пулеметчики стоят по периметру доски и «стреляют наружу».Докажем, что большее количество пулеметчиков расставить нельзя. Рассмотрим произвольную расстановку пулеметчиков, не бьющих друг друга. Внесем в нее следующие изменения: всех пулеметчиков, стоящих на краю доски, «развернем» так, чтобы они «стреляли» наружу; после этого каждого пулеметчика, стоящего не на краю доски, сдвинем на край в направлении его стрельбы. Ясно, что после этого пулеметчики будут стоять на разных клетках и не будут бить друг друга. Теперь все пулеметчики стоят на краю доски, значит, их не более 76.
Задача 5: f(x) – многочлен третьей степени. Докажите, что существует такое натуральное k, что многочлен f(x) + f(x + 1) + … + f(x + k) имеет ровно один вещественный корень.
(С.~Берлов, К.~Кохась)
Решение: Не умаляя общности, можно считать, что старший коэффициент многочлена положителен. Достаточно проверить, что существует k, для которого f′(x) + f′(x + 1) + … + f′(x + k) ≥ 0 при всех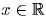 .
Заметим, что f′(x) – это некоторый квадратный трехчлен с положительным
коэффициентом при x². Если
.
Заметим, что f′(x) – это некоторый квадратный трехчлен с положительным
коэффициентом при x². Если  всех x, то утверждение
задачи очевидно, поэтому будем считать, что f′ имеет два вещественных
корня. Пусть s – расстояние между корнями этого трехчлена, m – модуль
его наименьшего (отрицательного) значения, t – число настолько большое,
что при |x| > t f′(x) > m(s + 1). В качестве k можно взять любое
натуральное число, большее, чем 2t + s + 1. В самом деле, среди чисел
x,x + 1, … ,x + k в этом случае отрицательных – не больше s + 1,
следовательно, сумма отрицательных слагаемых в выражении
f′(x) + f′(x + 1) + … + f′(x + k) по модулю не
превосходит (s + 1)m. С другой стороны, хотя бы одно из чисел
x,x + 1, … ,x + k по модулю больше t, поэтому сумма положительных
слагаемых в выражении f′(x) + f′(x + 1) + … + f′(x + k)
больше (s + 1)m. Это доказывает неравенство.
Задача 6: Вокруг остроугольного треугольника ABC описана окружность.
Высоты треугольника из вершин A и C пересекают окружность
в точках E и F соответственно, D – произвольная точка на (меньшей)
дуге AC, K – точка пересечения DF и AB, L – точка пересечения
DE и BC. Докажите, что прямая KL проходит через ортоцентр
треугольника ABC.
всех x, то утверждение
задачи очевидно, поэтому будем считать, что f′ имеет два вещественных
корня. Пусть s – расстояние между корнями этого трехчлена, m – модуль
его наименьшего (отрицательного) значения, t – число настолько большое,
что при |x| > t f′(x) > m(s + 1). В качестве k можно взять любое
натуральное число, большее, чем 2t + s + 1. В самом деле, среди чисел
x,x + 1, … ,x + k в этом случае отрицательных – не больше s + 1,
следовательно, сумма отрицательных слагаемых в выражении
f′(x) + f′(x + 1) + … + f′(x + k) по модулю не
превосходит (s + 1)m. С другой стороны, хотя бы одно из чисел
x,x + 1, … ,x + k по модулю больше t, поэтому сумма положительных
слагаемых в выражении f′(x) + f′(x + 1) + … + f′(x + k)
больше (s + 1)m. Это доказывает неравенство.
Задача 6: Вокруг остроугольного треугольника ABC описана окружность.
Высоты треугольника из вершин A и C пересекают окружность
в точках E и F соответственно, D – произвольная точка на (меньшей)
дуге AC, K – точка пересечения DF и AB, L – точка пересечения
DE и BC. Докажите, что прямая KL проходит через ортоцентр
треугольника ABC.
(С.~Берлов)
Решение: Обозначим через H ортоцентр ∆ ABC. Тогда ∠ AHF = ∠ EHC = ∠ ABC – как углы между высотами треугольника, ∠ AFC = ∠ HEC = ∠ ABC – как углы, опирающиеся на одну дугу. Значит, треугольники AFH и CHE равнобедренные (и подобные). Так как точки K и L лежат на высотах этих треугольников, то FK = KH и HL = LE, и, следовательно, ∠ KFH = ∠ KHF, ∠ LEH = ∠ LHE. Заметим еще, что ∠ AFD = ∠ AED как опирающиеся на одну дугу. Теперь осталось подвести итог всем нашим наблюдениям: ∠ KHF = ∠ AFC – ∠ AFD = ∠ EHC – ∠ EHL = ∠ LHC, т. е. углы FHK и LHC вертикальные. Значит, отрезки KH и HL лежат на одной прямой, что и требовалось доказать.Задача 7: Докажите, что в любой компании, состоящей из четного числа людей, найдутся два человека, у которых в этой компании четное число общих знакомых.
(М.~Антипов)
Решение: Допустим, что это не так, т. е. любые два человека имеют нечетное число общих знакомых. Разобьем всех людей на три группы. В первую группу возьмем произвольного человека, пусть это будет Вася. Во вторую группу возьмем всех Васиных знакомых, в третью – всех, кто с Васей незнаком. Рассмотрим подробнее вторую группу. Каждый человек из второй группы имеет нечетное число общих знакомых с Васей, причем все эти знакомые, конечно, находятся тоже во второй группе. Таким образом, каждый человек из второй группы знает нечетное число людей из второй группы. Отсюда следует, что во второй группе четное число людей. Кстати, мы установили, что у Васи четное число знакомых, а поскольку Вася – произвольно взятый человек, то у каждого человека в этой компании четное число знакомых.Рассмотрим теперь подробнее третью группу. Каждый человек из третьей группы имеет нечетное число общих знакомых с Васей, и, разумеется, все эти общие знакомые находятся во второй группе. Таким образом, каждый человек из третьей группы знаком с нечетным числом людей из второй группы (и незнаком с Васей). Поскольку у каждого человека четное число знакомых, мы можем заключить, что каждый человек из третьей группы знаком с нечетным числом людей из третьей группы. Значит, в третьей группе число людей тоже четно. Но тогда число людей во всех трех группах нечетно. Противоречие.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Городской тур >> 11 класс | Убрать решения |