 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Городской тур >> 8 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1995 года. Городской тур. 8 класс |
|
|
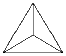
(Д.~Карпов)
Решение: При прибавлении единиц к числам на сторонах одного из треугольников их сумма увеличивается на три (что не влияет на остаток), а суммы в трех других треугольниках увеличиваются на единицу. Применим эту операцию к каждому треугольнику такое количество раз, которое равно начальному значению суммы чисел на его сторонах. После этого сумма чисел в каждом треугольнике будет давать при делении на три такой же остаток, как сумма начальных значений всех четырех сумм. Задача 2: В войске герцога Икторна 1000 гоблинов. Любые два гоблина либо дружат, либо враждуют, либо незнакомы. Гоблины – существа малообщительные, разговаривают только с друзьями. К тому же все они в плохом настроении, поскольку у каждого гоблина любые два его друга враждуют, а любые два врага дружат. Докажите, что для того, чтобы все войско узнало о предстоящем наступлении на Данвин, герцог должен сообщить об этом не менее чем 200 гоблинам.
(Р.~Семизаров)
Решение: Заметим, что никто из гоблинов не имеет больше двух друзей. Действительно, если какие-то трое дружат с одним и тем же гоблином, то они должны все враждовать между собой, что противоречит условию (двое, враждующие с третьим, должны дружить). Отсюда следует, что любой гоблин вместе со своими друзьями, друзьями своих друзей и так далее, образует цепочку (возможно, циклическую), в которой первый дружит со вторым, второй – с третьим и так далее. Рассмотрим фрагмент такой цепочки, состоящий из пяти гоблинов – A, B, C, D и E. Так как A и C – друзья B, они должны враждовать между собой; C и E – друзья D и тоже враждуют между собой. Значит, A и E дружат между собой, так как оба – враги C. Итак, каждый из этих пяти гоблинов уже имеет двоих друзей в той же компании, и следовательно, ни с кем больше не дружит. Таким образом, длина цепочки друзей не может быть больше пяти.Значит, один гоблин может передать новость (в том числе через других гоблинов) не более чем пятерым, считая и его самого. Значит, если герцог сообщит о наступлении меньше чем 200 гоблинам, то о нем узнают меньше, чем 200 • 5 = 1000 гоблинов, то есть не все войско.
Задача 3: Обозначим через p(n,k) количество делителей числа n, не меньших, чем k. Чему равна сумма p(1001,1) + p(1002,2) + p(1003,3) + … + p(2000,1000)\,?
(С.~Берлов)
Решение: Ответ: 2000. Для каждого натурального числа k от 1 до 1000 выпишем все делители числа 1000 + k, не меньшие k. Тогда искомая сумма равна общему количеству всех выписанных чисел. Докажем, что каждое число n от 1 до 2000 выписано ровно один раз. Если n больше 1000, то оно появляется в списке лишь как делитель самого себя. Если же n не превосходит 1000, то оно выписывается для таких k, что k ≤ n и 1000 + k делится на n, то есть ровно один раз, поскольку в интервале от 1001 до 1000 + n ровно одно число делится на n. Таким образом, выписаны все числа от 1 до 2000, причем по одному разу, то есть ровно 2000 чисел.Задача 4: BD – биссектриса угла B треугольника ABC. Точка E выбрана так, что ∠ EAB = ∠ ACB, AE = DC, и при этом отрезок ED пересекает отрезок AB в точке K. Докажите, что KE = KD.
(С.~Берлов)
Решение: Опустим перпендикуляры EX и DY на прямую AB, и DZ – на прямую BC. Имеем DY = DZ, так как BD – биссектриса угла ABC, и EX = DZ из равенства треугольников AEX и CDZ. Значит, EX = DY. Следовательно, треугольники KEX и KDY равны (по катету и острому углу). Отсюда KE = KD. Задача 5: Наследство состоит из нескольких бриллиантов и оценивается в 1\,000\,000 долларов. Известно, что его можно разделить на 5, а можно и на 8 равных частей. Какую наибольшую стоимость может иметь самый маленький бриллиант?
Ответ: 50000 (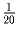 всего наследства).
всего наследства).
В качестве примера можно взять по четыре бриллианта стоимостей 50\,000, 75\,000 и 125\,000. Докажем, что наименьший бриллиант не может быть дороже 50\,000. При делении наследства на восемь равных частей по 125\,000 по крайней мере одна часть составлена из двух или более бриллиантов. Заменим каждый бриллиант, стоящий ровно 125\,000, на два бриллианта половинной стоимости – от этого ни стоимость наименьшего бриллианта, ни возможность разбиения на пять частей не изменятся. После этого в каждой части не меньше двух бриллиантов, то есть всего бриллиантов не меньше 16. Значит, при делении на пять частей по 200\,000 в какой-то части окажется по крайней мере четыре бриллианта, и уже в этой части один из бриллиантов стоит не дороже 50\,000.
(Ф.~Назаров)
Задача 6: В вершинах правильного стоугольника произвольным образом расставлены числа от 1 до 100. Разрешается поменять местами два числа, отличающиеся на 1. В результате выполнения таких операций каждое число передвинулось в соседнюю вершину по часовой стрелке. Докажите, что в какой-то момент менялись местами два числа, находившиеся в диаметрально противоположных вершинах.
(М.~Гусаров)
Решение: Предположим, что среди проведенных операций не было обмена чисел между двумя противоположными вершинами стоугольника. Рассмотрим две противоположные вершины A и B. Пусть в начальной расстановке число в вершине A было больше числа в вершине B. Тогда и на протяжении всего процесса число в вершине A будет больше числа в вершине B. (При каждой операции может измениться только одно из этих чисел, причем ровно на 1, так что оно не может стать больше другого, если было меньше, и наоборот.) Но в конце там стоят числа, изначально находившиеся в вершинах A′ и B′, соседних с A и B против часовой стрелки. Значит, в начале число в вершине A′ было больше числа в вершине B′. Применив то же рассуждение к A′ и B′, мы установим аналогичное неравенство для следующей пары противоположных вершин, и так далее. Двигаясь таким образом против часовой стрелки, мы снова дойдем до вершин A и B, причем окажется, что число в вершине B больше, чем в вершине A. Противоречие.Задача 7: Клетчатый прямоугольник разрезали на прямоугольники 1 × 2 (доминошки) так, что любая прямая, идущая не по линиям сетки параллельно одной из сторон, рассекает четное число доминошек. Докажите, что длина одной из сторон делится на 4.
(Д.~Карпов)
Решение: Можно считать, что вертикальная сторона прямоугольника имеет четную длину (обе стороны не могут быть нечетными, так как площадь четна). Если она не делится на 4, то дает при делении на 4 остаток 2. Тогда, как легко видеть, любой столбец задевает горизонтально расположенные доминошки в количестве, дающем остаток 2 при делении на 4.Отметим столбцы прямоугольника через один. Сложив количества горизонтальных доминошек, задеваемых отмеченными столбцами, мы получим общее число горизонтальных доминошек. Остаток этого числа при делении на 4 равен 2, если отмеченных столбцов нечетное число, и 0, если их четное число. Отсюда горизонтальная сторона должна быть четной – если она нечетна, то отмеченных столбцов может быть как четное, так и нечетное число (в зависимости от того, начинали мы отмечать с первого столбца или со второго), и количество горизонтальных доминошек получается разным при разных способах подсчета. Предположим, что горизонтальная сторона дает остаток 2 при делении на 4. Тогда число отмеченных столбцов нечетно, так что общее количество горизонтальных доминошек дает остаток 2 при делении на 4.
Теперь то же рассуждение, примененное к строкам вместо столбцов, показывает, что число вертикальных доминошек тоже дает остаток 2 при делении на 4. Значит, количество всех доминошек делится на 4. Следовательно, площадь прямоугольника делится на 8, откуда одна из сторон делится на 4.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Городской тур >> 8 класс | Убрать решения |