 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Городской тур >> 9 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1995 года. Городской тур. 9 класс |
|
|
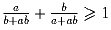 .
.
(Д.~Карпов)
Задача 2: На плоскости даны ∆ ABC и точки D и E, такие, что ∠ ADB = ∠ BEC = 90. Докажите, что длина отрезка DE не превосходит полупериметра ∆ ABC.(С.~Берлов)
Задача 3: Решите в натуральных числах уравнение: .
.
(Д.~Карпов)
Задача 4: Докажите, что количество способов разрезать прямоугольник на уголки из трех клеток вида всегда четно.
всегда четно.
(Д.~Карпов)
Задача 5: В четырехугольнике ABCD на сторонах BC и AD взяты, соответственно, точки R и T. P – точка пересечения отрезков BT и AR; S – точка пересечения отрезков CT и DR. Оказалось, что PRST – параллелограмм. Докажите, что AB || CD.
(Д.~Карпов, А.~Храбров)
Задача 6: a, b, c – натуральные числа, причем (a – b) – простое число и 3c² = c(a + b) + ab. Докажите, что 8c + 1 – точный квадрат.(С.~Берлов)
Задача 7: В государстве 2000 городов. Некоторые пары городов соединены дорогами так, что из любого города можно проехать в любой другой. Докажите, что это государство можно разбить на несколько республик (возможно, всего на одну) так, чтобы в каждой республике из любого города можно было единственным образом проехать в любой другой город этой республики, не выезжая за ее пределы. (В каждой республике должно быть не менее двух городов.)
(Д.~Карпов, А.~Пастор)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Городской тур >> 9 класс | Показать решения |