 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Отборочный тур >> 10 КЛАСС. | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1995 года. Отборочный тур. 10 класс |
|
|
(А.~Голованов)
Задача 2: На плоскости даны две пересекающиеся окружности. Точка A – одна из двух точек пересечения этих окружностей. В каждой окружности проведен диаметр, параллельный касательной в точке A к другой окружности, причем эти диаметры не пересекаются. Докажите, что концы этих диаметров лежат на одной окружности.(С.~Берлов )
Задача 3: На плоскости дано 1995 точек, некоторые пары точек соединены отрезками. Точки первоначально раскрашены в два цвета. Каждую минуту (одновременно) те точки, которые соединены с четным количеством точек такого же цвета, меняют свой цвет. Докажите, что исходная раскраска не сможет снова получиться через нечетное число минут.(С.~Берлов)
Задача 4: d1, d2,…,dk – все возможные натуральные делители некоторого натурального числа N, выписанные в порядке возрастания. Оказалось, что d2 – d1, d3 – d2, d4 – d3, …, dk – dk – 1 – также все возможные делители какого-то натурального числа (не обязательно в порядке возрастания). Найдите все N, для которых такое может быть.
(А.~Голованов)
Задача 5: В Цветочном городе живут 1995 коротышек. У них имеется 995 10-копеечных монет и неограниченный запас пятаков (монет по 5 коп.). Иногда коротышки меняются монетами: один дает другому монету в 10 копеек, а тот ему – два пятака. Как-то вечером каждый из коротышек заявил: «Сегодня я отдал ровно 10 монет». Докажите, что кто-то из них ошибся.(К.~Кохась)
Задача 6: H – ортоцентр остроугольного треугольника ABC; D – середина стороны AC. Прямая, проходящая через H перпендикулярно отрезку DH, пересекает стороны AB и BC в точках E и F. Докажите, что HE = HF.(С.~Берлов)
Задача 7: Найдите все простые p и q, для которых p² – p + 1 = q³.(А.~Голованов)
Задача 8: На доске написаны числа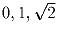 . Разрешается к любому из этих
чисел прибавить разность двух других, умноженную на произвольное рациональное
число. Можно ли такими операциями получить числа
. Разрешается к любому из этих
чисел прибавить разность двух других, умноженную на произвольное рациональное
число. Можно ли такими операциями получить числа 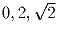 ?
?
(С.~Иванов)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Отборочный тур >> 10 КЛАСС. | Показать решения |