 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Отборочный тур >> 11 КЛАСС. | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1995 года. Отборочный тур. 11 класс |
|
|
(А.~Голованов)
Задача 2: Дан треугольник ABC. На продолжении стороны AB за точку B, на продолжении BC за точку C и на продолжении стороны CA за точку A выбраны точки B1, C1, A1 соответственно, так, что AB = BB1, BC = CC1, CA = AA1. Оказалось, что треугольник A1B1C1 – равносторонний. Докажите, что треугольник ABC – тоже равносторонний.
(Д.~Карпов)
Задача 3: a,b,c,d > 0. Докажите неравенство:(ac + bd)5 + (ad + bc)5 ≤ (a + b)5(c5 + d5)
(А.~Храбров)
Задача 4: Можно ли расставить по окружности числа от 1 до 25 так, чтобы сумма любых пяти стоящих подряд чисел давала при делении на 5 остаток 1 или 4?(Р.~Семизаров)
Задача 5: В Цветочном городе живут 1995 коротышек. У них имеется 995 10-копеечных монет и неограниченный запас пятаков (монет по 5 коп.). Иногда коротышки меняются монетами: один дает другому монету в 10 копеек, а тот ему – два пятака. Как-то вечером каждый из коротышек заявил: «Сегодня я отдал ровно 10 монет». Докажите, что кто-то из них ошибся.(К.~Кохась)
Задача 6: M – некоторое множество простых чисел, в котором больше одного элемента. Известно, что для всякого (конечного) подмножества N ⊂ M число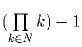 имеет простые делители только из M. Докажите, что M совпадает с
множеством всех простых чисел.
имеет простые делители только из M. Докажите, что M совпадает с
множеством всех простых чисел.
(А.~Пастор)
Задача 7: В остроугольном треугольнике ABC проведены высоты AA1 и BB1. На (меньшей) дуге AB описанной около треугольника окружности выбрана точка L, такая, что LC = CB. При этом оказалось, что ∠ BLB1 = 90. Докажите, что высота AA1 делится высотой BB1 пополам.(С.~Берлов)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Отборочный тур >> 11 КЛАСС. | Показать решения |