 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Отборочный тур >> 9 КЛАСС | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1995 года. Отборочный тур. 9 класс |
|
|
(А.~Голованов)
Задача 2: a,b,c > 0. Докажите неравенство: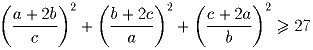
(Д.~Карпов)
Задача 3: На плоскости даны две пересекающиеся окружности. Точка A – одна из двух точек пересечения этих окружностей. В каждой окружности проведен диаметр, параллельный касательной в точке A к другой окружности, причем эти диаметры не пересекаются. Докажите, что концы этих диаметров лежат на одной окружности.(С.~Берлов )
Задача 4: На плоскости дано 1995 точек, некоторые пары точек соединены отрезками. Точки первоначально раскрашены в два цвета. Каждую минуту (одновременно) те точки, которые соединены с четным количеством точек такого же цвета, меняют свой цвет. Докажите, что исходная раскраска не сможет снова получиться через нечетное число минут.(С.~Берлов)
Задача 5: Пусть M – множество значений многочлена x² + 1 в целых точках. Докажите, что множество M не содержит ни одной бесконечной (непостоянной) геометрической прогрессии.(А.~Голованов)
Задача 6: Прямоугольник разбит на доминошки (т. е. прямоугольники 1 × 2). Докажите, что его клетки можно раскрасить в два цвета так, чтобы любая доминошка в данном разбиении содержала клетки разных цветов, но в любом другом разбиении этого прямоугольника на доминошки нашлась бы доминошка, содержащая две клетки одного цвета.(Д.~Карпов)
Задача 7: H – ортоцентр остроугольного треугольника ABC; D – середина стороны AC. Прямая, проходящая через H перпендикулярно отрезку DH, пересекает стороны AB и BC в точках E и F. Докажите, что HE = HF.(С.~Берлов)
Задача 8: Существует ли возрастающая последовательность натуральных чисел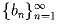 такая, что при всех натуральных n сумма цифр
числа
такая, что при всех натуральных n сумма цифр
числа 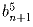 равна числу
равна числу 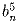 ?
?
(Д.~Давыдок, Д.~Карпов)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Отборочный тур >> 9 КЛАСС | Показать решения |