 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Районный тур >> 6 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1995 года. Районный тур. 6 класс |
|
|
Примечание: «Сумма произведений чисел по строкам» получается так: в каждой строке все числа перемножаются и четыре полученных произведения складываются; другая сумма получается аналогично.
(Д.~Карпов)
Решение: Например:1 вариант:

2 вариант:

(Можно подобрать расстановку, в которой все числа различны).
Задача 2: В лесу, состоящем из дубов и елок, компания «Пень-Инвест» вырубила одну треть всех дубов и одну шестую всех елок [соотв. 1/12 и 1/4]. Докажите, что отчет экологической организации «Зеленый мститель», утверждающий, что была вырублена половина [треть] всех деревьев, содержит неверные данные.
(Жюри)
Решение: В лесу вырубили менее половины [трети] дубов и менее половины [трети] елок. Значит, вырублено менее половины [трети] деревьев. Задача 3: Пятизначное число A записывается только двойками и тройками, а пятизначное число B – только тройками и четверками. Может ли произведение AB записываться одними двойками? Не забудьте обосновать свой ответ.[Пятизначное число A записывается только единицами и двойками, пятизначное число B – только двойками и тройками. Может ли AB записываться одними шестерками?]
(С.~Берлов)
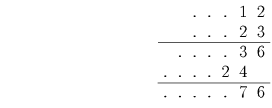
Решение: Варианты не аналогичны.1 вариант: Произведение этих чисел заключено в промежутке от 22222 • 33333 до 33333 • 44444, т. е. от 740725926 до 1481451852. Поэтому первая цифра произведения – не 2.
2 вариант: Чтобы произведение оканчивалось на 6, необходимо, чтобы первый сомножитель оканчивался на 2, а второй – на 3. Последние две цифры произведения однозначно определяются последними двумя цифрами сомножителей. Легко проверить, что ни одно из произведений – 12 на 23, 12 на 33, 22 на 23 и 22 на 33 – не оканчивается на 66.
(А.~Голованов)
Решение: Ответ: нет.Решение 1. Если бы из числа 1 можно было получить число 74 [78], то, выполняя операции перестановки цифр и деления четного числа на 2, из числа 74 [78] можно было бы получить 1. Попробуем: перестановка цифр приводит только к числу 47 [87], которое на два не делится, так что дальнейшие действия с ним не дадут ничего нового; деление числа 74 [78] на два дает нам число 37 [39], которое само нечетно, и полученное из него перестановкой цифр число 73 [93] тоже нечетно. Таким образом, попытка выполнить обратные преобразования приводит к получению всего трех новых чисел, среди которых нет единицы.
Решение 2. При выполнении операций количество цифр числа не уменьшается, поэтому если мы получили число, состоящее из трех или более цифр, то дальнейшие действия с ним никогда больше не приведут нас к двузначному числу. На схеме приведены все возможные способы применения операций, начинающиеся с числа 1 и до того момента, пока не получается трехзначное число. Как видим, число 74 [78] получить нельзя.
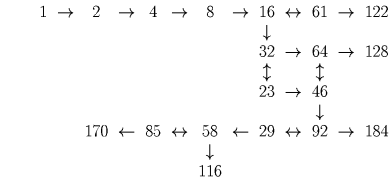
Решение 3 (для второго варианта): заметим, что указанные операции не могут из числа, не делящегося на 3, сделать число, на 3 делящееся.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Районный тур >> 6 класс | Убрать решения |