 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Районный тур >> 8 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1995 года. Районный тур. 8 класс |
|
|
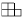 [
[ ]
(сторона клетки на рисунке равна единице). Докажите, что его можно разрезать
на прямоугольники 1 × 5 [1 × 3].
]
(сторона клетки на рисунке равна единице). Докажите, что его можно разрезать
на прямоугольники 1 × 5 [1 × 3].
(Д.~Карпов)
Задача 2: Можно ли в таблице 3 × 3 расставить числа 3, 4, 5, …, 11 [4, 5, 6, …, 12] так, чтобы произведение чисел первой строки было равно произведению чисел первого столбца, произведение чисел второй строки было равно произведению чисел второго столбца, и, наконец, произведение чисел третьей строки было равно произведению чисел третьего столбца?
(А.~Храбров)
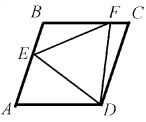
Задача 3: Точки E и F лежат, соответственно, на сторонах AB и BC ромба ABCD, причем AE = 5 • BE, BF = 5 • CF [BE = 7 • AE, CF = 7 • BF]. Известно, что треугольник DEF – равносторонний. Найдите величину угла BAD [ABC].
(Д.~Карпов)
Задача 4: Каких пятизначных чисел больше: четных с суммой цифр, равной 36, или нечетных с суммой цифр, равной 38? Не забудьте обосновать ответ. [Каких пятизначных чисел с суммой цифр, равной 37, больше: четных или нечетных?]
(А.~Голованов)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Районный тур >> 8 класс | Показать решения |