 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Районный тур >> 8 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1995 года. Районный тур. 8 класс |
|
|
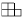 [
[ ]
(сторона клетки на рисунке равна единице). Докажите, что его можно разрезать
на прямоугольники 1 × 5 [1 × 3].
]
(сторона клетки на рисунке равна единице). Докажите, что его можно разрезать
на прямоугольники 1 × 5 [1 × 3].
(Д.~Карпов)
Решение: Площадь данного прямоугольника делится нацело на площадь указанной фигурки, то есть на 5 [3]. Площадь прямоугольника равна произведению длин сторон. Поскольку длины сторон – целые числа, а 5 [3] – простое число, то длина одной из сторон должна делится на 5 [3]. Разделим эту сторону и противоположную ей на отрезки длины 5 [3], а две другие стороны – на отрезки длины 1, после чего соединим соответствующие точки на противоположных сторонах прямыми линиями.Задача 2: Можно ли в таблице 3 × 3 расставить числа 3, 4, 5, …, 11 [4, 5, 6, …, 12] так, чтобы произведение чисел первой строки было равно произведению чисел первого столбца, произведение чисел второй строки было равно произведению чисел второго столбца, и, наконец, произведение чисел третьей строки было равно произведению чисел третьего столбца?
(А.~Храбров)
Решение: Да, можно. 1 вариант:
2 вариант:

(Д.~Карпов)
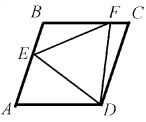
Решение: Ответы: в первом варианте – 60, во втором – 120.Из условия задачи (в обоих вариантах) следует, что BE = CF. Отложим на стороне AB отрезок AK, равный BE. Треугольники ADK и CDF равны по двум сторонам и углу (AD = CD, AK = CF, ∠ DAK = ∠ DCF). Значит, DK = DF = DE, то есть треугольник DKE – равнобедренный. В частности, равны углы DKE и DEK при его основании. Следовательно, треугольники ADK и BDE равны (по двум сторонам и углу: AK = BE, DK = DE, ∠ DKA = ∠ DEB). Отсюда AD = BD, то есть треугольник ABD – равносторонний. Следовательно, ∠ BAD = 60, ∠ ABC = 120.

Задача 4: Каких пятизначных чисел больше: четных с суммой цифр, равной 36, или нечетных с суммой цифр, равной 38? Не забудьте обосновать ответ. [Каких пятизначных чисел с суммой цифр, равной 37, больше: четных или нечетных?]
(А.~Голованов)
Решение: Ответы: в первом варианте больше четных чисел с суммой цифр 36, во втором варианте нечетных чисел с суммой цифр 37 больше, чем четных.Решение первого варианта: легко видеть, что пятизначное число с суммой цифр 38 не может иметь в своей записи нулей (в противном случае сумма цифр не превосходила бы суммы четырех девяток, то есть 36). Из каждого нечетного числа с суммой цифр 38 можно получить четное число с суммой цифр 36, уменьшив на 1 две его последние цифры. При этом из разных нечетных чисел получаются разные четные. Однако некоторые четные числа с суммой цифр 36 (например, 99990) не могут быть получены в результате такой операции. Таким образом, установлено взаимно однозначное соответствие между всеми нечетными числами с суммой цифр 38 и некоторыми (но не всеми!) четными числами с суммой цифр 36. Следовательно, первых меньше, чем вторых.
Второй вариант задачи решается аналогично: четному числу с суммой цифр 37 ставится в соответствие нечетное посредством увеличения на 1 последней цифры и уменьшения на 1 предпоследней цифры.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Районный тур >> 8 класс | Убрать решения |