 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Районный тур >> 9 класс. | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1995 года. Районный тур. 9 класс |
|
|
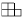 [
[ ]
(сторона клетки на рисунке равна единице). Докажите, что его можно разрезать
на прямоугольники 1 × 5 [1 × 3].
]
(сторона клетки на рисунке равна единице). Докажите, что его можно разрезать
на прямоугольники 1 × 5 [1 × 3].
(Д.~Карпов)
Решение: Площадь данного прямоугольника делится нацело на площадь указанной фигурки, то есть на 5 [3]. Площадь прямоугольника равна произведению длин сторон. Поскольку длины сторон – целые числа, а 5 [3] – простое число, то длина одной из сторон должна делится на 5 [3]. Разделим эту сторону и противоположную ей на отрезки длины 5 [3], а две другие стороны – на отрезки длины 1, после чего соединим соответствующие точки на противоположных сторонах прямыми линиями.Задача 2: Решите в вещественных числах систему уравнений

(А.~Храбров)
Решение: Ответ: система имеет единственное решение: a = b = c = d = 0. Сложив два уравнения системы, получим уравнение 8a² + 9b² + 7c² + 4d² = 16ab + 8cd Из неравенств 2ab ≤ a² + b² и 2cd ≤ c² + d² следует, что правая часть этого уравнение не больше левой, и равенство может достигаться только если b = 0, c = 0, a = b и c = d. Значит, единственным возможным решением данной системы является a = b = c = d = 0.Второй вариант решается аналогично.
Задача 3: В ромбе ABCD на сторонах AB и BC взяты, соответственно, точки E и F, такие, что CF/BF = BE/AE = 1994 [1995]. Оказалось, что DE = DF. Найдите величину угла EDF.
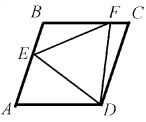
Из условия задачи (в обоих вариантах) следует, что BE = CF. Отложим на стороне AB отрезок AK, равный BE. Треугольники ADK и CDF равны по двум сторонам и углу (AD = CD, AK = CF, ∠ DAK = ∠ DCF). Значит, DK = DF = DE, то есть треугольник DKE – равнобедренный. В частности, равны углы DKE и DEK при его основании. Следовательно, треугольники ADK и BDE равны (по двум сторонам и углу: AK = BE, DK = DE, ∠ DKA = ∠ DEB). Отсюда AD = BD, то есть треугольник ABD – равносторонний. Следовательно, ∠ BAD = 60, ∠ ABC = 120.

(А.~Храбров)
Решение: Пусть команда А победила команду Б в матче с такими правилами (возможно, обеспечив себе победу досрочно). Это значит, что при любом мыслимом исходе оставшихся (непробитых) пенальти результат команды А был бы выше, чем команды Б. Представим себе, что команды продолжили пробивание пенальти после окончания матча и пробили все оставшиеся пенальти, причем команда А не забила больше ни одного мяча, а команда Б больше ни разу не промахнулась. При этом общее количество мячей, забитых А, все равно останется больше, чем забитых Б (именно это и значат слова «досрочная победа»). На сколько же оно может быть больше? Только на 1 или на 2. Действительно, если бы разница оказалась больше двух, то победа команды А стала бы неизбежной еще раньше, перед пробиванием последней пары пенальти.Далее, заметим, что при рассматриваемом нами продолжении матча в ворота попала ровно половина всех ударов. Таким образом, и из всех 129 [130] пар ударов в ворота попала ровно половина, то есть ровно 129 [130]. Эти 129 [130] голов делятся между А и Б так, что у А на 1 или на 2 больше. Это однозначно определяет число мячей, забитых командой А – 65 [66].
Задача 5: Решите уравнение в натуральных числах:
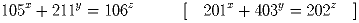
(Д.~Карпов)
Решение: У данного уравнения имеется единственное решение: x = 2, y = 1, z = 2 (в обоих вариантах). То, что оно является решением, следует из общего тождества a² + (2a + 1) = (a + 1)²\,, применяемого в первом варианте к a = 105, а во втором – к a = 201.Других решений нет, так как если z > 2, то правая часть уравнения делится на 8, а левая – нет, поскольку 105x [201x] может давать при делении на 8 только остаток 1, а 211y [403y] – только остатки 1 и 3. Осталось заметить, что при z = 1 решений также нет, а при z = 2 однозначно определены значения y = 1 и x = 2.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Районный тур >> 9 класс. | Убрать решения |