 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1998 >> Городской тур >> 11 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1998. Городской тур. 11 класс |
|
|
Найдите все положительные решения уравнения
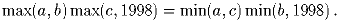
(А.~Храбров)
Задача 2:Натуральное число n таково, что n + 1 делится на 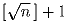 .
Докажите, что (n – 1)(n – 3) делится на
.
Докажите, что (n – 1)(n – 3) делится на 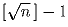 .
.
(А.~Голованов)
Задача 3: Задача 4:Две плоскости делят куб на четыре равновеликие части. Докажите, что его поверхность они тоже делят на четыре равновеликие части.
(М.~Гусаров)
Задача 5:Докажите, что для любого натурального n выполнено неравенство
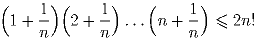
(Ю.~Базлов)
Задача 6:В клетках квадрата 8 × 8 расставлены целые числа. Каждая клетка закрыта карточкой, на которой написана сумма чисел в квадрате 3 × 3 с центром в этой клетке. Какое наибольшее количество чисел в клетках квадрата можно заведомо определить, если известны только числа на карточках?
(С\.~Волченков)
Задача 7:| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1998 >> Городской тур >> 11 класс | Показать решения |