 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1998 >> Отборочный тур >> 11 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1998. Отборочный тур. 11 класс |
|
|
В куче 666 спичек. Два игрока ходят по очереди. Каждый своим ходом может либо взять из кучи от 1 до 5 спичек, либо обменять у судьи ранее взятые 5 спичек на ириску. Выигрывает взявший последнюю спичку. Кто выиграет при правильной игре?
(К.~Кохась)
Задача 2:Окружность, проходящая через вершины A и C треугольника ABC, пересекает сторону AB в ее середине D, а сторону BC – в точке E. Окружность, проходящая через точку E и касающаяся в точке C прямой AC, пересекает прямую DE в точке F. K – точ- ка пересечения прямых AC и DE. Докажите, что прямые CF, AE и BK пересекаются в одной точке.
(С.Берлов)
Задача 3:Можно ли в «клетчатом» кубе 8 × 8 × 8 отметить 64 клетки так, чтобы в каждом слое кубиков, параллельном грани, было отмечено ровно 8 клеток, а среди любых 8 отмеченных клеток какие-то две обязательно находились в одном таком слое?
(А.~Вершик)
Задача 4:Найдите все многочлены P(x,y) от двух переменных такие, что при любых x и y P(x + y,y – x) = P(x,y).
(А.~Голованов)
Задача 5:2n-угольник A1A2 … A2n вписан в окружность с центром O и радиусом 1. Докажите, что
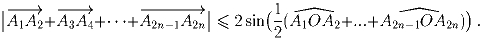
(Ю.~Базлов)
Задача 6:Пусть d(n) обозначает количество натуральных делителей числа n. Докажите, что последовательность d(n² + 1) ни с какого места не становится строго монотонной.
(А.~Голованов)
Задача 7:В дружине 169 человек. Каждый день четверо из них выходят на дежурство. Может ли через некоторое время случиться, что любые двое отдежурили вместе ровно один раз?
(К.~Кохась)
Задача 8:Можно ли в клетках таблицы 11 × 11 так расставить буквы П, А, С, чтобы в верхней строчке таблицы было написано: «ПАПАСПАСПСА», ни одна из остальных клеток, прилегающих к границе, не содержала бы букву С и чтобы ни в одной фигурке вида triminougolok (при любой её ориентации) не было трех различных букв?
(Н.~Филонов)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1998 >> Отборочный тур >> 11 класс | Показать решения |