 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1998 >> Отборочный тур >> 9 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1998. Отборочный тур. 9 класс |
|
|
На сколько нулей может оканчиваться число
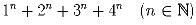 ?
?
(А.~Храбров)
Задача 2:Диагонали параллелограмма ABCD пересекаются в точке O. Окружность, описанная вокруг треу- гольника ABO, пересекает сторону AD в точке E. Окружность, описанная вокруг треугольника DOE, пересекает отрезок BE в точке F. Докажите, что ∠ BCA = ∠ FCD.
(С.Берлов)
Задача 3:На листе клетчатой бумаги нарисована несамопересекающаяся замкнутая ломаная, не проходящая через узлы сетки. В области, ограниченной ломаной, лежит не менее 91 узла. Докажите, что ломаная пересекает линии сетки по крайней мере в 40 точках.
(С.~Иванов)
Задача 4:Докажите, что количество таких натуральных чисел
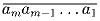 (m > 1998), что
(m > 1998), что
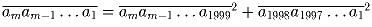 , — четно.
, — четно.
(А.~Храбров)
Задача 5:В квадрате 10 × 10 расставлены все натуральные числа от 1 до 100. В каждой строке отметили третье по величине число (считая от наибольшего). Докажите, что сумма всех отмеченных чисел не меньше суммы чисел в некоторой строке.
(С.Берлов)
Задача 6:Докажите, что проекции точки пересечения диагоналей вписанного четырехугольника на две его противоположные стороны симметричны относительно прямой, соединяющей середины двух других противоположных сторон этого четырехугольника.
(С.Берлов)
Задача 7:Множество M состоит из n точек плоскости, никакие три из которых не лежат на одной прямой. Для каждого треугольника с вершинами из M подсчитали количество точек M внутри него. Докажите, что среднее арифметическое всех найденных чисел не превосходит n/4.
(С.~Иванов)
Задача 8:На очень большом столе лежат две кучи спичек. В первой куче 2¹ºº спичек, во второй – 3¹ºº. Два игрока по очереди берут спички из куч. Одним ходом разрешается брать из одной кучи k спичек, из другой – m так, чтобы |k² – m²| ≤ 1000. Выигрывает взявший последнюю спичку. Кто выиграет при правильной игре?
(С.Берлов)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1998 >> Отборочный тур >> 9 класс | Показать решения |