Задача 1:

В записи четырех десятизначных чисел все цифры – восьмерки и девятки. Докажите, что можно добавить к ним пятое десятизначное число, также записываемое только восьмерками и девятками, так, чтобы сумма всех пяти чисел записывалась только четными цифрами.

(К. Кохась)

Задача 2:

На сторонах AB и BC треугольника ABC взяты точки D и E соответственно такие, что 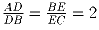и  ∠ ACB = 2 ∠ DEB. Докажите, что треугольник ABC равнобедренный.

(Д.~Карпов)

Задача 3:

Задача 4:

Можно ли числа от 1 до 1999 разбить на несколько групп таким образом, чтобы в каждой группе сумма двух наибольших чисел в 9 раз превосходила сумму оставшихся?

(К. Кохась)

Задача 6:

Диагональ AC выпуклого четырехугольника ABCD делится точкой пересечения диагоналей пополам. Известно, что  ∠ ADB = 2 ∠ CBD. На диагонали BD нашлась такая точка K, что CK = KD + AD. Докажите, что  ∠ BKC = 2 ∠ ABD.

(Ф.\,Бахарев, С.\,Берлов)

Задача 7:

Последовательность x_n такова, что x₁ = 1, а каждый следующий член вычисляется по формуле

Докажите, что в этой последовательности встретятся 1000 членов подряд, делящихся на 3. (Через [a] обозначается наибольшее целое число, не превосходящее a.)

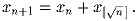
(Д.~Карпов)

Задача 8:

В мэрии города N работают 200 честных сотрудников и k взяточников. В день рождения мэра каждый сотрудник отправил ему анонимное письмо, в котором перечислил ровно k взяточников. При этом честные сотрудники перечислили k истинных взяточников, а взяточники могли обвинить любых сотрудников мэрии. При каких k мэр заведомо сможет только на основании этих данных разоблачить хотя бы одного взяточника?

(Ю.\,Лифшиц)