 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1999 >> Городской тур >> 9 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1999. Городской тур. 9 класс |
|
|
Докажите, что не существует натуральных чисел x и y
и простого числа p таких, что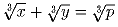 .
.
(А.~Храбров)
Задача 2:На острове Новая Вавилония используются 45 языков, причем каждый житель знает по крайней мере пять из них. Известно, что любые два жителя могут вести между собой беседу, возможно при посредничестве нескольких переводчиков. Докажите, что тогда любые два островитянина смогут поговорить между собой, пользуясь услугами не более чем 15 переводчиков.
(С.Берлов)
Задача 3:В неравнобедренном треугольнике ABC проведены биссектрисы AA1 и CC1, кроме того отмечены середины K и L сторон AB и BC соответственно. Точка P — основание перпендикуляра, опущенного из вершины A на прямую CC1, а точка Q — основание перпендикуляра, опущенного из вершины C на прямую AA1. Докажите, что прямые KP и LQ пересекаются на стороне AC.
(Ф.Бахарев)
Задача 4:В песочнице лежит кучка из 123456789 песчинок. Дима и Катя играют в следующую игру. За один ход можно взять из любой кучки любое число песчинок, большее 1, которое является делителем числа песчинок в этой кучке, и создать из них отдельную кучку. Первый ход делает Катя. Проигрывает тот игрок, который не может сделать ход. Кто выиграет при правильной игре?
(Е.~Сопкина, Д.~Ростовский)
Задача 5:На стороне BC остроугольного треугольника ABC взята точка K. Биссектриса угла CAK вторично пересекает окружность, описанную около треугольника ABC, в точке L. Докажите, что, если прямая LK перпендикулярна отрезку AB, то либо AK = KB, либо AK = AC.
(С.Берлов)
Задача 6:Натуральные числа a, b, c и d таковы, что a² + b² + ab = c² + d² + cd\,. Докажите, что число a + b + c + d — составное.
(С.~Иванов)
Задача 7:В кабинете Мюллера стоит сейф, ячейки которого расположены в виде квадрата 100 × 100. В 25 ячейках хранятся важные секретные материалы. Штирлицу удалось установить, в каких именно, и послать в Центр шифровку в виде последовательности из 25 чисел от 1 до 100. Докажите, что Штирлиц и Центр могли заранее согласовать способ шифровки так, чтобы сотрудники Центра, изучив шифровку, смогли выбрать 400 ячеек, среди которых заведомо находятся 25 нужных.
(А.~Храбров)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1999 >> Городской тур >> 9 класс | Показать решения |