 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1999 >> Отборочный тур >> 11 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1999. Отборочный тур. 11 класс |
|
|
Под куполом цирка летают красные, синие и зеленые воздушные шары — по 150 каждого цвета. Внутри каждого синего шара находится ровно 13 зеленых, внутри каждого красного — ровно 5 синих и ровно 19 зеленых. Докажите, что какой-то зеленый шарик не содержится ни в одном из 449 остальных шаров.
(С.~Иванов)
Задача 2:Задача 3:
(an) — арифметическая прогрессия, состоящая из натуральных чисел,
pn — наибольший простой
делитель an при каждом натуральном n. Докажите, что последовательность
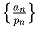 неограничена.
неограничена.
(А.~Голованов)
Задача 4:На 50 карточках с двух сторон написаны (по разу) все натуральные числа от 1 до 100. Карточки выложены на стол так, что видны только числа, написанные сверху. Вася может выбрать несколько карточек и одновременно перевернуть их, а затем сложить все 50 чисел, которые окажутся после этого наверху. Каково наибольшее S, для которого Вася может наверняка получить сумму, не меньшую S?
(С.Берлов)
Задача 5:Два человека играют в следующую игру. Они по очереди выписывают на доску делители числа 100!, (кроме 1, без повторений). Проигрывает тот из игроков, после чьего хода написанные на доске числа будут взаимно просты в совокупности. Кто выиграет при правильной игре: начинающий или его противник?
(Д.~Карпов)
Задача 6: Задача 7:В связном графе G 500 вершин, степень каждой вершины не превосходит 3. Назовем раскраску вершин в черный и белый цвета интересной/, если белым цветом окрашено более половины вершин, но никакие две белые вершины не соединены ребром. Докажите, что можно выбрать несколько вершин G так, чтобы в любой интересной раскраске больше половины из них были бы окрашены в черный цвет.
(Д.~Карпов)
Задача 8:Три фокусника показывают фокус. Они дают зрителю колоду карточек с числами от 1 до 2n + 1 (n > 6). Зритель берет себе одну карточку, а остальные раздает поровну (произвольным образом) первому и второму фокусникам. Фокусники, не общаясь, изучают каждый свои n карт, отбирают из них по 2 карты, и, сложив их в (упорядоченную) стопочку, передают третьему фокуснику. Третий фокусник просматривает полученные 4 карты и сообщает, какая карта у зрителя. Объясните, каким образом может быть показан такой фокус.
(К. Кохась)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1999 >> Отборочный тур >> 11 класс | Показать решения |