 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2000 >> Городской тур >> 10 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 2000. Городской тур. 10 класс |
|
|
Последовательности x1,x2, … и y1,y2, …
заданы условиями x1 = ⅛,  ,
,
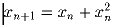 ,
, 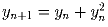 .
Докажите, что числа xm и yn не равны ни при каких натуральных
m и n.
.
Докажите, что числа xm и yn не равны ни при каких натуральных
m и n.
(А.~Голованов)
Задача 2:AA1 и BB1 — высоты остроугольного треугольника ABC. Точки K и M — середины отрезков AB и A1B1 соответственно. Отрезки AA1 и KM пересекаются в точке L. Докажите, что точки A, K, L и B1 лежат на одной окружности.
Задача 3: Задача 4:Число N равно произведению 200 различных натуральных чисел. Докажите, что N имеет не меньше 19901 различных натуральных делителей (включая единицу и само число).
(А.~Голованов)
Задача 5:Клетки квадрата 2000 × 2000 закрашивают по следующим правилам. В любой момент можно закрасить одиночную клетку, если ни одна из соседних с ней клеток еще не закрашена; или прямоугольник 1 × 2, если к этому моменту уже закрашены ровно две из соседних с ним клеток; или квадрат 2 × 2, если уже закрашены 8 соседних с ним клеток. (Соседними считаются клетки, примыкающие по стороне.) Можно ли закрасить весь квадрат?
(К. Кохась)
Задача 6:Одна из вневписанных окружностей треугольника ABC касается стороны AB и продолжений сторон CA и CB в точках C1, B1 и A1 соответственно. Другая вневписанная окружность касается стороны AC и продолжений сторон BA и BC в точках B2, C2 и A2 соответственно. Прямые A1B1 и A2B2 пересекаются в точке P, прямые A1C1 и A2C2 — в точке Q. Докажите, что точки A, P и Q лежат на одной прямой.
(С.~Берлов)
Задача 7:Будем называть натуральное число «почти простым», если оно не делится ни на одно простое число из интервала [3,19]. Будем называть число «очень непростым», если оно имеет хотя бы два простых делителя из интервала [3,19]. Какое наибольшее количество почти простых чисел можно выбрать так, чтобы любые два из них в сумме давали очень непростое число?
(С.~Берлов, С.~Иванов)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2000 >> Городской тур >> 10 класс | Показать решения |