 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2000 >> Отборочный тур >> 11 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 2000. Отборочный тур. 11 класс |
|
|
Существует ли квадратный трехчлен f с положительными коэффициентами такой, что для любого положительного числа x имеет место равенство [f(x)] = f([x]). (Квадратные скобки, как обычно, обозначают целую часть числа.)
(А.~Храбров)
Задача 2:За какое наименьшее число взвешиваний на чашечных весах с делениями можно упорядочить гири весом в 1, 3, 3², …, 326 г? (Чашечные весы с делениями позволяют определять разность весов грузов, лежащих на чашках.)
(О.Ванюшина)
Задача 3:Задача 4:
Прямая 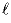 — касательная к окружности, описанной вокруг
остроугольного треугольника ABC, проведенная в точке B. Точка K —
проекция ортоцентра треугольника на прямую
— касательная к окружности, описанной вокруг
остроугольного треугольника ABC, проведенная в точке B. Точка K —
проекция ортоцентра треугольника на прямую 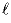 , а точка L —
середина стороны AC. Докажите, что треугольник BKL — равнобедренный.
, а точка L —
середина стороны AC. Докажите, что треугольник BKL — равнобедренный.
(Ф.~Бахарев)
Задача 5:В квадрате 1 × 1 с единичными скоростями летают два шарика. Между собой они никак не взаимодействуют, а от стенок отскакивают по закону «угол падения равен углу отражения». Докажите, что с верхней стороны на нижнюю может с единичной скоростью спуститься паучок на паутинке так, что ни его, ни паутинку за время опускания шарики не заденут.
(К.~Пименов)
Задача 6:Докажите, что для любых положительных чисел, удовлетворяющих условию x1 ≤ x2 ≤ … ≤ xn, справедливо неравенство
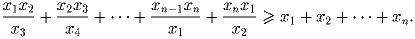
(А.~Храбров)
Задача 7:На плоскости дан выпуклый n-угольник P, ограничивающий площадь меньше 1. Для каждой точки X на плоскости определяется величина F(X), равная площади объединения всевозможных отрезков, соединяющих X с точками многоугольника (площадь выпуклой оболочки/). Доказать, что множество точек X, для которых F(X) = 1, является выпуклым многоугольником с не более чем 2n сторонами.
(Ю.~Бураго)
Задача 8:Какое наименьшее количество единичных отрезочков нужно стереть в клетчатом прямоугольнике 2000 × 3000 (граничные отрезки стирать запрещается) так, чтобы никакие из оставшихся не образовывали прямоугольника меньшего размера?
(А.~Храбров, Д.~Ростовский)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2000 >> Отборочный тур >> 11 класс | Показать решения |