 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2000 >> Районный тур >> 7 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 2000. Районный тур. 7 класс |
|
|
На доске написано три двузначных числа, одно из которых начинается на 5, второе — на 6, а третье — на 7. Учитель попросил трех учеников, чтобы каждый из них выбрал какие-нибудь два из этих чисел и сложил их. Может ли так быть, что у первого ученика получилось 147, а ответы второго и третьего — различные трехзначные числа, начинающиеся на 12?
(Р. Семизаров)
Задача 2:В группе из 50 ребят некоторые знают все буквы, кроме «р», которую просто пропускают при письме, а остальные — знают все буквы, кроме «к», которую тоже пропускают. Однажды учитель попросил 10 учеников написать слово «кот», 18 других учеников — слово «рот», а остальных — слово «крот». При этом слова «кот» и «рот» оказались написанными по 15 раз. Сколько ребят написали свое слово верно?
(Р. Семизаров)
Задача 3:В выпуклом четырехугольнике ABCD AB = BC. Лучи BA и CD пересекаются в точке E, а лучи AD и BC – в точке F. Известно, что BE = BF и ∠ DEF = 25. Hайдите ∠ EFD.
(М.~Пратусевич)
Задача 4:Бумажный прямоугольник размером 6 × 11 клеток разрезали
на фигурки вида 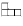 и
и 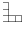 ,, после чего одну из фигурок потеряли.
Докажите, что из оставшихся фигурок, использовав их все, невозможно
составить «по клеточкам» прямоугольник.
Фигурки можно поворачивать и переворачивать, но нельзя накладывать друг на
друга.
,, после чего одну из фигурок потеряли.
Докажите, что из оставшихся фигурок, использовав их все, невозможно
составить «по клеточкам» прямоугольник.
Фигурки можно поворачивать и переворачивать, но нельзя накладывать друг на
друга.
(Жюри)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2000 >> Районный тур >> 7 класс | Показать решения |