Задача 1: В каждой клетке таблицы 10 × 10 написано натуральное число, не превосходящее 10. При этом числа в любых двух соседних (через сторону или угол) клетках взаимно просты. Докажите, что какое-то число встречается в таблице не менее 17 раз.

(Ю.Лифшиц)

Задача 2:

Биссектрисы углов A и B выпуклого четырехугольника ABCD пересекаются в точке P, а биссектрисы углов C и D — в точке Q, отличной от P. Прямая PQ проходит через середину стороны AB. Докажите, что  ∠ ABC =  ∠ BAD или  ∠ ABC +  ∠ BAD = 180.

(С.Берлов)

Задача 3:

Существуют ли такие квадратные трехчлены f и g с единичными старшими коэффициентами, что для любого целого n число f(n)g(n) — целое, а числа f(n), g(n) и f(n) + g(n) — нецелые?

(А.Храбров)

Задача 4:

На плоскости дано 10 точек, занумерованных числами от 1 до 10. Можно провести любую ориентированную прямую, спроектировать на нее эти точки и, если все проекции различны, выписать в ряд номера точек в том порядке, в котором проекции расположены на прямой. Какое набольшее число перестановок чисел от 1 до 10 может получаться таким способом из одного набора точек на плоскости?

(С.Иванов)

Задача 5:

На доске написано натуральное число. Два игрока ходят по очереди, и каждый своим ходом заменяет написанное на доске число n числом n – 1 или 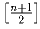. Выигрывает тот, кто первым напишет на доске число 1. В начале игры число на доске равно 1,000,000. Кто выиграет при правильной игре: начинающий или его партнер?

Задача 6:

Высоты остроугольного треугольника ABC пересекаются в точке H. Точка K такова, что описанные окружности треугольников BHK и CHK касаются прямой BC. Точка D — основание высоты, опущенной из вершины B на сторону AC. Докажите, что точка A равноудалена от прямых KB и KD.

(С.Берлов)

Задача 7:

Пусть  σ (n) обозначает сумму всех натуральных делителей числа n. Докажите, что уравнение  σ (n)^k = n^m не имеет решений в натуральных числах при n > 1.

Задача 8:

В стране n городов, из некоторых ведут дороги в города той же страны или за границу (при этом два города могут соединяться более чем одной дорогой). Известно, что из любого города выходит не более n дорог, и из любых двух городов, не соединенных между собой, выходит в сумме не более n дорог. Докажите, что всего дорог (внешних и внутренних) не более n(n + 1)/2.

(А.Федотов)