 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2001 >> Отборочный тур >> 9-10 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 2001. Отборочный тур. 9-10 класс |
|
|
(Ю.Лифшиц)
Решение:Предположим, что это не так, то есть каждое число встречается не более 16 раз. Разобьём таблицу на 25 квадратиков 2 × 2. В каждом из них не может быть более одного чётного числа и более одного числа, делящегося на три. Это означает, что всего чисел делящихся на 2 или 3 в таблице не более 50. Чисел же не делящихся ни на 2 ни на 3 всего три штуки (это 1, 5 и 7), поэтому на них приходится не более 3 • 16 = 48 клеток таблицы. То есть всего занято не более 50 + 48 = 98 клеток.
Задача 2:Биссектрисы углов A и B выпуклого четырехугольника ABCD пересекаются в точке P, а биссектрисы углов C и D — в точке Q, отличной от P. Прямая PQ проходит через середину стороны AB. Докажите, что ∠ ABC = ∠ BAD или ∠ ABC + ∠ BAD = 180.
(С.Берлов)
Решение:Если прямые BC и AD параллельны, то ∠ ABC + ∠ BAD = 180, так как эти углы являются соответственными. Пусть эти прямые пересекаются в точке E.
Заметим, что точка Q равноудалена от прямых BC и AD: она равноудалена от AD и CD, так как лежит на биссектрисе ∠ ADC и равноудалена от CD и BC так как лежит на биссектрисе ∠ DCB. Это означает, что точка Q лежит на биссектрисе ∠ E. Аналогичным образом проверяется, что и точка P лежит на биссектрисе угла E. Но это означает, что середина стороны AB также ледит на биссектрисе угла E, а отсюда, в свою очередь, следует, что треугольник AEB равнобедренный. Поскольку ∠ ABC и ∠ BAD являются внутренними или внешними (в зависимости от положения точки E) углами при основании треугольника AEB, то они равны.
Задача 3:
Существуют ли такие квадратные трехчлены f и g с единичными старшими коэффициентами, что для любого целого n число f(n)g(n) — целое, а числа f(n), g(n) и f(n) + g(n) — нецелые?
(А.Храбров)
Решение: Да, такие трёхчлены существуют, причём возможных примеров довольно много. Один из них –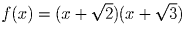 ,
,  .
Доказательство того, что они удовлетворяют условию, представляет собой не
очень сложное упражнение.
Задача 4:
.
Доказательство того, что они удовлетворяют условию, представляет собой не
очень сложное упражнение.
Задача 4: На плоскости дано 10 точек, занумерованных числами от 1 до 10. Можно провести любую ориентированную прямую, спроектировать на нее эти точки и, если все проекции различны, выписать в ряд номера точек в том порядке, в котором проекции расположены на прямой. Какое набольшее число перестановок чисел от 1 до 10 может получаться таким способом из одного набора точек на плоскости?
(С.Иванов)
Решение:Заметим, что если две прямые сонаправлены, то порядок проекций точек на них совпадает. Рассмотрим теперь окружность, содержащую все эти точки. Любая прямая сонаправлена одной из касательных (направление касательные – по часовой стрелке).
Проведём прямую через какие-то две данные точки, пусть она пересекла окружность в точках A и B. Порядок, в котором проекции точки будут находится на касательной, зависит от того, на какой из дуг AB окажется точка касания.
Проведя прямые через каждую пару точек, заметим, что они разобьют окружность
на 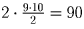 дуг. Каждая дуга соответствует
своему порядку точек, значит всего различных порядков
не более 90, а если никакие из проведённых прямых не совпадают, то
их ровно 90. Остаётся привести пример расположения точек, при котором
никакие три не лежат на одной прямой.
дуг. Каждая дуга соответствует
своему порядку точек, значит всего различных порядков
не более 90, а если никакие из проведённых прямых не совпадают, то
их ровно 90. Остаётся привести пример расположения точек, при котором
никакие три не лежат на одной прямой.
На доске написано натуральное число.
Два игрока ходят по очереди, и каждый своим ходом заменяет
написанное на доске число n числом n – 1 или 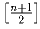 .
Выигрывает тот, кто первым напишет на доске число 1.
В начале игры число на доске равно 1,000,000.
Кто выиграет при правильной игре: начинающий или его партнер?
.
Выигрывает тот, кто первым напишет на доске число 1.
В начале игры число на доске равно 1,000,000.
Кто выиграет при правильной игре: начинающий или его партнер?
Будем называть выигрышными те числа, при которых тот, чья очередь хода, выигрывает, а проигрышными – все остальные числа. Из проигрышных чисел можно получить только выигрышные, а из любого выигрышного можно получить прогрышное. Докажем по индукции, что все чётные числа выигрышны.
Число 2 выигрышно. Пусть теперь число k = 2m проигрышно, а все меньшие чётные числа выигрышны. Тогда числа 2m – 1 и m выигрышны. По индукционному предположению выигрышно таже число 2m – 2. Выходит, что из выигрышного числа 2m – 1 можно получить только выигрышные числа 2m – 2 и m, а этого быть не может.
Задача 6:
Высоты остроугольного треугольника ABC пересекаются в точке H. Точка K такова, что описанные окружности треугольников BHK и CHK касаются прямой BC. Точка D — основание высоты, опущенной из вершины B на сторону AC. Докажите, что точка A равноудалена от прямых KB и KD.
(С.Берлов)
Задача 7:Пусть σ (n) обозначает сумму всех натуральных делителей числа n. Докажите, что уравнение σ (n)k = nm не имеет решений в натуральных числах при n > 1.
Задача 8:
В стране n городов, из некоторых ведут дороги в города той же страны или за границу (при этом два города могут соединяться более чем одной дорогой). Известно, что из любого города выходит не более n дорог, и из любых двух городов, не соединенных между собой, выходит в сумме не более n дорог. Докажите, что всего дорог (внешних и внутренних) не более n(n + 1)/2.
(А.Федотов)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2001 >> Отборочный тур >> 9-10 класс | Убрать решения |