Задача 1:
Задача 2:
Костя задумал натуральное число, перемножил все его цифры и результат умножил
на задуманное число. Получилось 1716. Какое число задумал Костя?
Найдите все возможные ответы и докажите, что других ответов нет.
Задача 3:
Дети гуляют во дворе детского сада. Тех из них, у кого на ногах надето
поровну носков, в 5 раз меньше, чем тех, у кого не поровну. Воспитательница
велела детям переодеться, и каждый ребенок снял с одной ноги носок и надел
его на другую ногу. Теперь тех, у кого носков на ногах поровну, стало в 2
раза меньше, чем тех, у кого не поровну. Могло ли быть так, что в начале
прогулки более чем у половины детей на одной ноге было ровно на один носок
меньше, чем на другой?
У тех, у кого носков было поровну
(их была 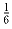 часть), станет не поровну.
Кроме того, у тех, у кого на одной ноге было ровно на один носок меньше, чем на другой,
после переодевания также тоже будет не поровну носков.
Поэтому, если их больше половины, то более чем у
часть), станет не поровну.
Кроме того, у тех, у кого на одной ноге было ровно на один носок меньше, чем на другой,
после переодевания также тоже будет не поровну носков.
Поэтому, если их больше половины, то более чем у
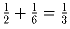 будет не поровну носков.
будет не поровну носков.
(К. Кохась)
Задача 4:
Вдоль правой стороны дороги припарковано 100 машин. Среди них —
30 красных, 20 желтых и 20 розовых мерседесов. Известно, что
никакие два мерседеса разного цвета не стоят рядом. Докажите, что тогда
какие-то три мерседеса, стоящие подряд, — одного цвета.
(К. Кохась)


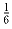 часть), станет не поровну.
Кроме того, у тех, у кого на одной ноге было ровно на один носок меньше, чем на другой,
после переодевания также тоже будет не поровну носков.
Поэтому, если их больше половины, то более чем у
часть), станет не поровну.
Кроме того, у тех, у кого на одной ноге было ровно на один носок меньше, чем на другой,
после переодевания также тоже будет не поровну носков.
Поэтому, если их больше половины, то более чем у
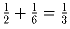 будет не поровну носков.
будет не поровну носков.