 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2001 >> Районный тур >> 8 класс >> I вариант | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 2001. Районный тур. 8 класс. I вариант |
|
|
Решение:
Сумма любых 12 чисел подряд равна 90. Т.,е. если из суммы всех чисел вычесть сумму любых двух стоящих подряд, получится 90. Значит, суммы любых двух чисел подряд одинаковы и равны 15. Поэтому каждое число меньше 15.
Задача 2: В лавке можно обменять шило на мыло, или 3 мыла на 1 шило, или 1 мыло на 4 шила (но не наоборот). После нескольких обменов у Сережи оказалось столько же шила и мыла, сколько было вначале. Докажите, что количество сделанных обменов делится на 16.
(С.Иванов)
Решение:Пусть первая смена шила на мыло происходила a раз, смена
3 мыл на шило – b раз, и мыла на четыре шила – c раз.
Поскольку количество мыла
у Серёжи не изменилось, то a – 3b – c = 0. Точно также, отслежива
операции с шилом, имеем, что – a + b + 4c = 0. Складывая эти два уравнения,
получаем, что 3c – 2b = 0, то есть 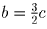 , а значит c –
чётное число. Из первого уравнения
, а значит c –
чётное число. Из первого уравнения 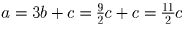 .
.
И, наконец,  . Поскольку c,
чётно, это означает, что a + b + c делится на 16.
. Поскольку c,
чётно, это означает, что a + b + c делится на 16.
Задача 3: На сторонах AB и BC треугольника ABC с углом ∠ C = 40 выбраны точки D и E такие, что ∠ BED = 20. Докажите, что AC + EC > AD.
(А.Пастор)
Решение: Продолжим сторону AC за точку C и отложим отрезок CF = CE. Тогда ∠ EFC = 20 градусов, AF = AC + CE. Угол FDA — внешний в треугольнике BED, поэтому он больше 20. В треугольнике AFD сторона AD лежит против меньшего угла, чем сторона AF. Поэтому AF > AD.Задача 4: Можно ли клетчатый бумажный квадрат 14 × 14 клеток разрезать «по клеточкам» на несколько прямоугольников, каждый из которых имеет размеры 2 × 5 или 3 × 9 клеток?
(Д.Карпов)
Решение:Пусть прямоугольников 2 × 5 – a штук, а прямоугольников 3 × 9 – b штук. Площадь квадрата равна 196 клеточек, значит 196 = 10a + 27b. Отсюда следует, что 27b заканчивается на 6, но минимальное такое число 27 • 8 = 216, что больше 196. То есть разбить квадрат требуемым образом не удастся.
Задача 5: Найдите все тройки натуральных чисел x, y, z такие, что xyz = 170170 и x²y + y²z + z²x = xy² + yz² + zx².
(Ф.Бахарев)
Решение: Ответ: (1,1,170170), (1, 170170, 1), (170170, 1, 1).170170 = 2 • 5 • 7 • 11 • 13 • 17 — свободно от квадратов. Второе уравнение раскладывается на множители: (x – y)(y – z)(z – x) = 0. Если, скажем, x = y, то 170170 делится на x², что возможно лишь при x = 1. Тогда y = 1, z = 170170.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2001 >> Районный тур >> 8 класс >> I вариант | Убрать решения |