 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Олимпиада ЮМШ >> 1999 год >> Заочный тур >> 5 - 7 класс | Показать решения |
|
|
| Санкт-Петербургские (Ленинградские) соревнования. Олимпиада ЮМШ. 1999 год. Заочный тур. 5 - 7 класс |
|
|
Найдите четырехзначное число, сумма цифр которого равна разности между числом 2034 и самим числом. Найдите все такие числа и покажите, что других таких чисел нет.
Задача 2:Трое детей решили две задачи, после чего каждый из них сделал два заявления об ответах, которые у них получились в этих задачах:
Первый: "В первой задаче ответ больше 18. Во второй – не больше 14."
Второй: "В первой получается меньше 20, а во второй – 14."
Третий: "В первой ответ – 15, а во второй ответ больше 14."
Известно, что один из них оба раза ошибся, а два других оба раза были правы. Какие ответы в этих задачах, если известно, что это – целые числа?
Задача 3:На одну из клеток шахматной доски высадился отряд из 64 десантников с целью захватить всю доску. Каждый день в каждой из клеток, в которых находятся десантники, происходит следующее: половина отряда отправляется в какую-либо не захваченную клетку, находящуюся на той же вертикали или на той же горизонтали. При этом проходить через клетки, в которых десантники уже стоят – запрещено. Если отряд в какой-либо клетке не может разделиться, в этой клетке начинаются учения и все солдаты в ней погибают. Покажите, что независимо от того, в какую клетку был выброшен десант, через 6 дней солдаты смогут захватить каждый по клетке.
Задача 4:На доске было записано несколько примеров. На перемене хулиган Паша заменил все цифры буквами, причем одинаковые цифры заменил одинаковыми буквами, а разные – разными. После этого запись стала выглядеть так, как это показано на рисунке. В начале следующего урока учитель попросил Пашу сосчитать сумму ответов в этих примерах. Чему может быть равна эта сумма? Приведите все варианты и докажите, что других нет.
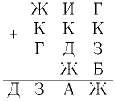
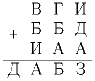

Задача 5:
Маленький мальчик постоянно узнает новые слова. По рабочим дням (с понедельника по пятницу) его родители на работе и он за день узнает всего 7 слов, в выходные же дни он узнает по 13 новых слов. Однако, каждое десятое слово, которое он узнает, является синонимом ровно одного из предыдущих. Мальчик родился в понедельник утром. К какому количеству слов он не будет знать синонимы через 100 дней после своего рождения?
Задача 6:Даны 30 гирь массами 1 г, 2 г,..., 30 г. Убрали 16 гирь таких, что их общая масса равна трети массы всех гирь. Всегда ли можно оставшиеся гири разделить на две кучки одинакового веса?
Задача 7:Используя цифры 1, 2,…, 9 не более чем по одному разу сделайте два четырехзначных числа с минимальной разностью.
Задача 8:
Сколькими способами можно вырезать из квадрата 9 × 9 квадрат 3 × 3 так, чтобы оставшееся можно было разрезать на прямоугольники 2 × 3?
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Олимпиада ЮМШ >> 1999 год >> Заочный тур >> 5 - 7 класс | Показать решения |