Задача 1:
Точечный прожектор освещает угол 45°. Какое наименьшее
количество прожекторов можно поставить внутри квадратной площадки
так, чтобы полностью ее осветить? На границу квадрата прожекторы
ставить нельзя.
Задача 2:
Решить уравнение:
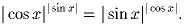
Задача 3:
В прямоугольнике 3 × 4 произвольным образом отмечено 6
точек. Докажите, что среди них обязательно найдутся две точки,
расстояние между которыми не превышает

.
Задача 4:
На доске записано N (N > 5) натуральных чисел. Наибольшее из них не
превышает 1996, а у любых пяти из них есть общий делитель, отличный от
1. Докажите, что все записанные на доске числа имеют общий делитель,
отличный от 1.


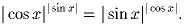
 .
.