 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVI олимпиада, 1995-1996 >> Областной тур >> 10 класс >> 1-й день | Убрать решения |
|
|
| XXXVI Екатеринбургская городская олимпиада, 1995-1996. Областной тур. 10 класс. 1-й день |
|
|
Решение: Тремя прожекторами осветить всю площадку нельзя, так как в этом случае какой-то прожектор должен освещать 2 угла, а значит полностью освещать некоторую сторону. Но тогда он должен находится на окружности, описанной около квадрата, что невозможно.
Четырех прожекторов хватит. В самом деле, если разместить прожекторы в точках пересечения вписанной окружности с диагоналями квадрата, то каждый прожектор полностью осветит противолежащую ему четверть площадки.
Ответ: 4 прожектора.
Задача 2: Решить уравнение: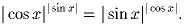
Решение:
В случаях | cos x | = 1 и cos x = 0 уравнение решений не
имеет. Если | cos x | = | sin x | , то имеем
cos ²x = sin ²x, cos 2x = 0,  . При 0 < | sin x | < | cos x | < 1 имеем
. При 0 < | sin x | < | cos x | < 1 имеем
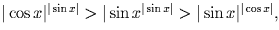 и уравнение корней не
имеет. Наконец, при 0 < | cos x | < | sin x | < 1
аналогично получаем
и уравнение корней не
имеет. Наконец, при 0 < | cos x | < | sin x | < 1
аналогично получаем 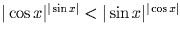 .
.
Ответ: 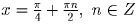 .
.
 .
.Решение:
Разобьем прямоугольник на единичные квадраты (cм. рис.8).
Eсли в некотором прямоугольнике 1 × 2 лежат две точки,
то расстояние между ними не больше  . Пусть в любом
таком прямоугольнике не более одной точки. Тогда хотя бы одна точка
попадет в один из закрашенных квадратов (так как остальная
часть разбивается на 5 прямоугольников 1 × 2),
а значит в некотором квадрате 3 × 3 окажутся остальные 5
точек. Разобьем этот квадрат средними линиями на 4 квадрата,
с диагональю
. Пусть в любом
таком прямоугольнике не более одной точки. Тогда хотя бы одна точка
попадет в один из закрашенных квадратов (так как остальная
часть разбивается на 5 прямоугольников 1 × 2),
а значит в некотором квадрате 3 × 3 окажутся остальные 5
точек. Разобьем этот квадрат средними линиями на 4 квадрата,
с диагональю 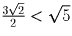 каждый. В некоторый такой
квадрат обязательно попадут 2 точки, которые и будут искомыми.
каждый. В некоторый такой
квадрат обязательно попадут 2 точки, которые и будут искомыми.
Решение: Предположим противное, то есть пусть у чисел a1, a2, … , aN нет общего делителя. Рассмотрим число a1. Так как оно не превосходит 1996 < 2*3*5*7*11 = 2310, среди его делителей не более 4 простых. Пусть p1, p2, p3, p4 – его простые делители, и пусть ni (1 ≤ i ≤ 4) – такие номера, что
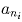 не делятся на pi (такие номера найдутся,
так как pi не является общим делителем чисел a1, a2, … , aN). Тогда пятерка чисел
не делятся на pi (такие номера найдутся,
так как pi не является общим делителем чисел a1, a2, … , aN). Тогда пятерка чисел 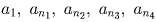 не может иметь общего делителя,
отличного от 1, вопреки условию.
не может иметь общего делителя,
отличного от 1, вопреки условию.Примечание. Как видно из доказательства, в условии задачи достаточно было полагать, что наименьшее из чисел не превосходит 1996.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVI олимпиада, 1995-1996 >> Областной тур >> 10 класс >> 1-й день | Убрать решения |